DISEGNANDO: METODO GENERALE

 Disegno
Mar 122022
 

Il METODO GENERALE, è una procedura grafica con la quale è possibile disegnare qualunque poligono regolare, utilizzando lo stesso metodo. Non è possibile definire in questo caso la dimensione del lato del poligono, bensì si dovrà partire dal diametro del cerchio che inscrive il poligono da disegnare.

Per rendere più semplice la procedura, sarà opportuno, fare in modo che il diametro del cerchio, sia sempre un multiplo del numero dei lati del poligono da disegnare. Quindi, ad esempio, se dobbiamo disegnare un pentagono, ossia un poligono di 5 lati, la dimensione del cerchio che lo inscrive dovrà essere un multiplo di questi lati, ossia misurare 10, 15, 20,…. cm, perché in questo modo sarà più facile poterlo dividere secondo il procedimento grafico. Se il poligono è un esagono (6 lati), il diametro del cerchio potrà essere 12,18,….cm. Stessa procedura per l’ettagono, ottagono, ecc.

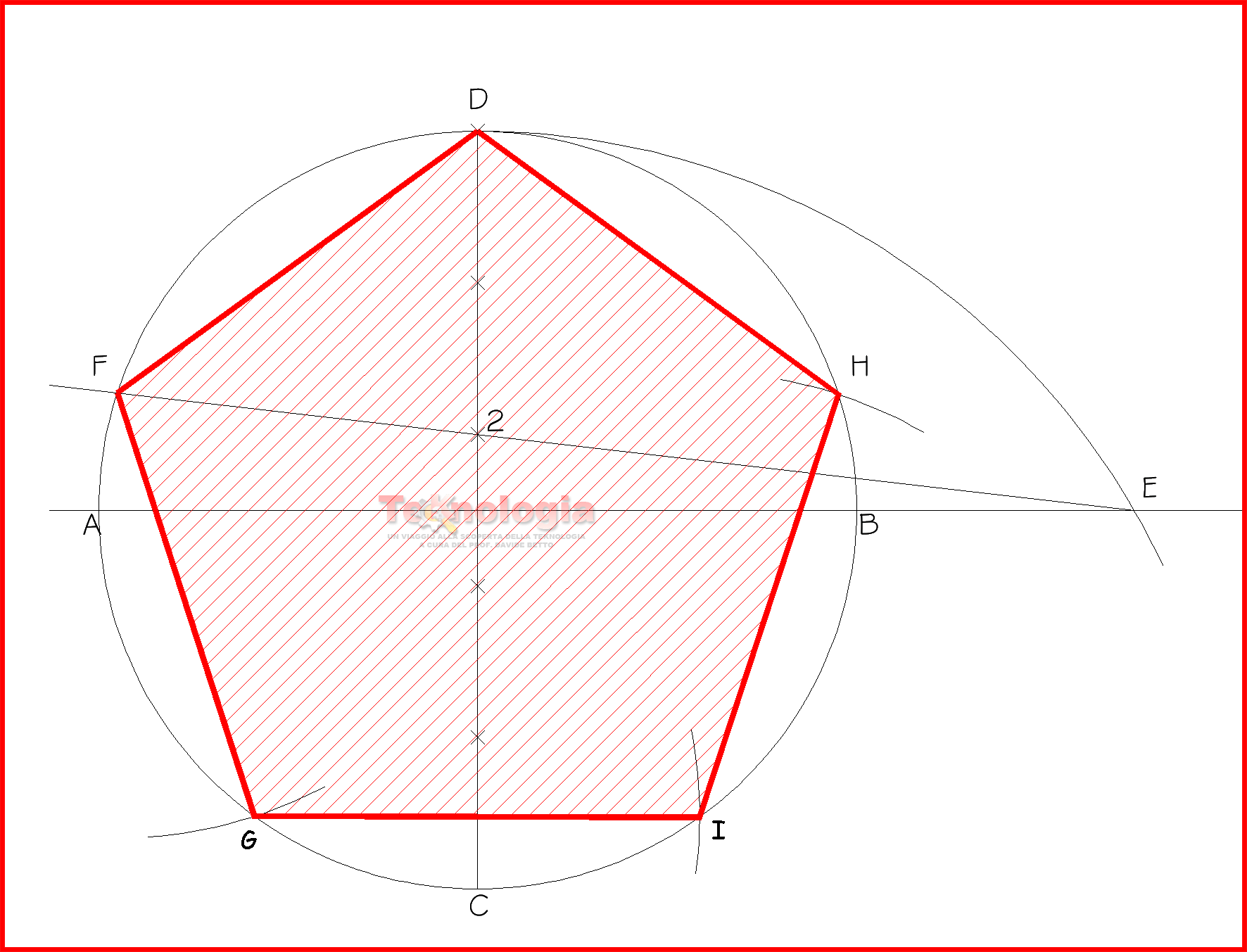
METODO GENERALE: PENTAGONO
Dati DIAMETRO CIRCONFERENZA  AB = MULTIPLO DI 5
STRUMENTI NECESSARI:
OPERAZIONI INIZIALI:

Usando un foglio F4, posizionato in orizzontale, effettuiamo le squadrature secondo gli schemi indicati in SQUADRATURA F/4.

PROCEDURA OPERATIVA:
  1. dividiamo con una linea orizzontale r il foglio in 2 parti uguali;
  2. puntiamo il compasso sulla linea r leggermente a sinistra rispetto al punto medio della retta e tracciamo una circonferenza del diametro stabilito (10cm o 15cm) che intersecherà la retta nei punti A e B;
  3. tracciamo dal centro della circonferenza una retta s, perpendicolare a r che intersecherà la circonferenza nei punti C e D;
  4. dividiamo ora il segmento CD in un numero di parti pari al numero di lati del pentagono ossia in 5 e numeriamole partendo dall’alto con 1, 2, 3, 4 e 5;
  5. puntiamo il compasso in C e con apertura CD (pari al diametro dl cerchio), tracciamo un arco di circonferenza che intersecherà la retta orizzontale r in un punto E;
  6. uniamo ora E con il punto 2 sul segmento CD (il punto 2 è il secondo tratto in cui abbiamo diviso CD) e prolunghiamo questa retta fino ad incontrare la circonferenza nel punto F;
  7. la distanza DF rappresenta la lunghezza di uno dei lati del pentagono. Essendo il pentagono una figura regolare, ossia con lati e angoli tutti uguali, apriamo il compasso con lunghezza DF e puntandolo su F tracciamo un archetto che interseca la circonferenza in un punto G;
  8. puntiamo ora il compasso in D con la stessa apertura DF e tracciamo un archetto che interseca la circonferenza in un punto H;
  9. infine, puntiamo il compasso su H sempre con la stessa apertura (DF) e tracciamo un archetto che interseca la circonferenza in un punto I;
  10. uniamo i punti DFGIH; otterremo il PENTAGONO costruito con il metodo detto generale.
VIDEO TUTORIAL:

METODO GENERALE: ESAGONO
Dati DIAMETRO CIRCONFERENZA  AB = MULTIPLO DI 6
ALTRE FIGURE:

ETTAGONO

OTTAGONO

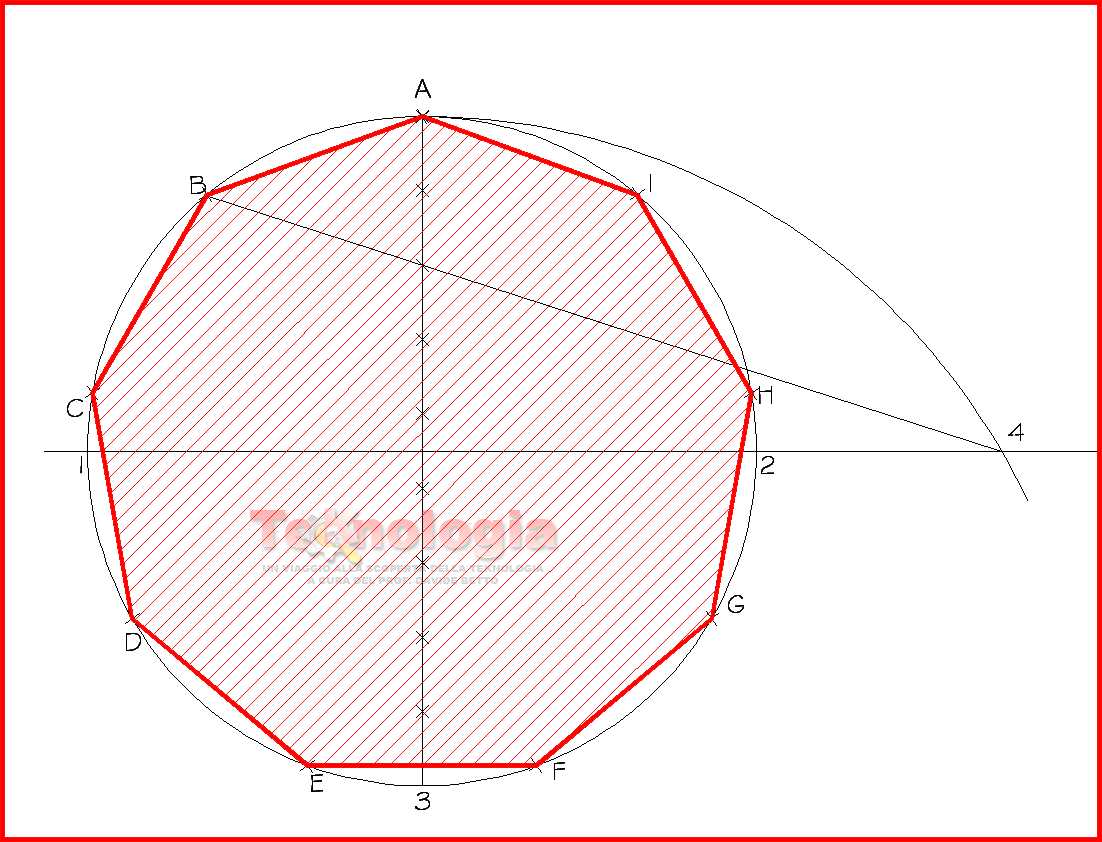
ENNAGNO