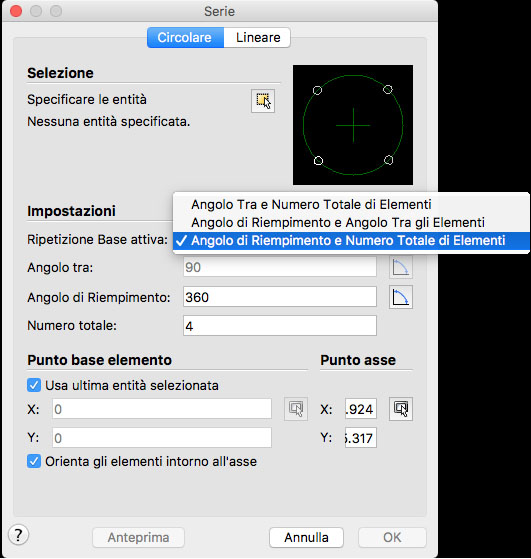
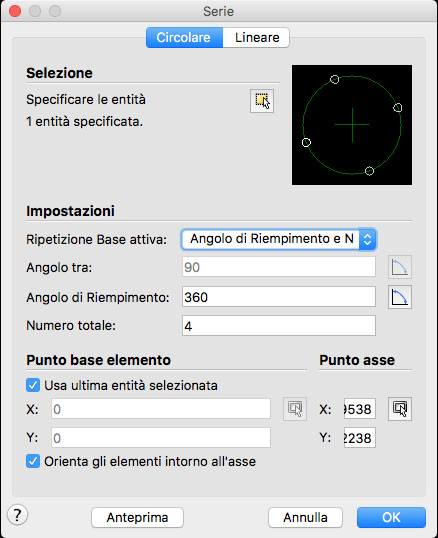
Tutto quello che noi disegniamo è basato su semplici segni grafici, ma se li osserviamo attentamente ci renderemo subito conto che si tratta di soli due simboli: la retta e il cerchio. E’ proprio grazie a questi due “segni” che, è nata e si è sviluppata una disciplina chiamata geometria, il cui nome deriva dalle parole del greco antico “geo = terra” e “metria = misura“. Si trattava della disciplina che si occupava della misurazione dei terreni, oggi divenuta una scienza scienza matematica che studia le forme nel piano e nello spazio.
I primi geometri, erano gli agrimensori dell’antico Egitto, coloro che si occupavano materialmente di effettuare queste misurazioni. In pratica, tendendo delle funi, riuscivano a tracciare sul terreno rette e cerchi e questa pratica rimase per molti secoli inalterata oltre che l’unico sistema conosciuto.
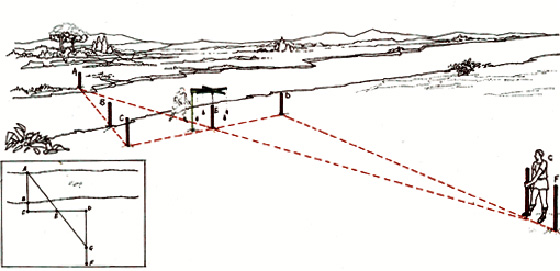
Agrimensore e misurazione di un campo
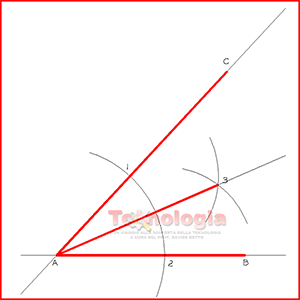
Gli agrimensori, effettuavano operazioni definite in gergo come “tirare una retta” o “descrivere un cerchio”, ma restavano comunque delle azioni empiriche. La scientificità di queste procedure divenne tale grazie ad Euclide che riuscì a trasferire queste conoscenze sui fogli di carta o sui libri utilizzando strumenti di disegno come la riga e il compasso.
 A questi strumenti se ne aggiunsero poi altri più complessi che consentirono di realizzare e disegnare curve ben più complesse delle rette o dei cerchi. La cosa interessante, nell’uso di questi strumenti non era tanto il risultato rappresentato sul supporto da disegno, bensì quello che consentivano lo spostamento di un punto lungo una direzione specifica, senza che il profilo di quest’ultima fosse materialmente presente.
A questi strumenti se ne aggiunsero poi altri più complessi che consentirono di realizzare e disegnare curve ben più complesse delle rette o dei cerchi. La cosa interessante, nell’uso di questi strumenti non era tanto il risultato rappresentato sul supporto da disegno, bensì quello che consentivano lo spostamento di un punto lungo una direzione specifica, senza che il profilo di quest’ultima fosse materialmente presente.
Le curve possono giacere su un piano o muoversi nello spazio, avendo quindi caratteristiche molto diverse. Quelle di cui ci occuperemo in questo articolo, vengono chiamate sezioni coniche perché derivano tutte dall’intersezione tra un piano e un cono e sono di conseguenza curve piane.
 Per comprendere quali curve è possibile ottenere, basta immaginare una parete di fronte a noi (il piano) colpita dal cono di luce prodotto da una torcia elettrica.
Per comprendere quali curve è possibile ottenere, basta immaginare una parete di fronte a noi (il piano) colpita dal cono di luce prodotto da una torcia elettrica.
In base all’inclinazione della torcia rispetto alla parete, è facile dimostrare e sperimentare che è possibile ottenere 4 differenti tipi di curva: circonferenza, ellissi, parabola e iperbole. Scopriamole insieme e vediamo quali sono le loro caratteristiche.
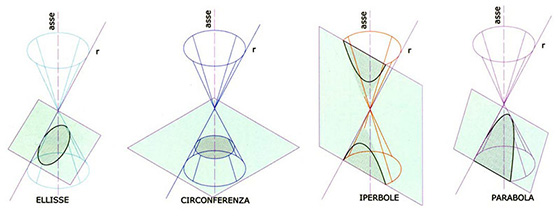

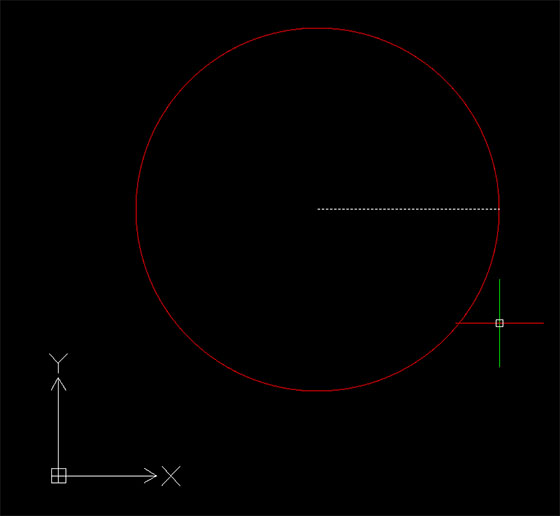
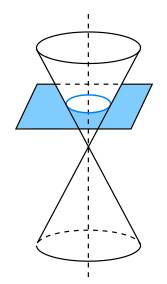 Se puntiamo una torcia perpendicolarmente ad una parete, il suo cono luminoso genererà su di essa una luce esattamente circolare, quindi definirà una curva che chiamiamo circonferenza. E’ come se tagliassimo un cono (v. immagine a sinistra) con un piano orizzontale perpendicolare al suo asse.
Se puntiamo una torcia perpendicolarmente ad una parete, il suo cono luminoso genererà su di essa una luce esattamente circolare, quindi definirà una curva che chiamiamo circonferenza. E’ come se tagliassimo un cono (v. immagine a sinistra) con un piano orizzontale perpendicolare al suo asse.
DEFINIZIONE:
“si definisce circonferenza, il luogo dei punti di un piano equidistanti da un punto detto centro della circonferenza“.
Gli elementi importanti che definiscono una circonferenza, sono:
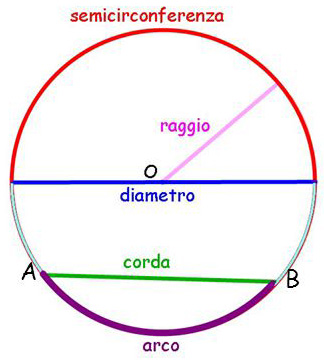 raggio, il segmento che unisce il centro della circonferenza con qualsiasi punto della circonferenza;
raggio, il segmento che unisce il centro della circonferenza con qualsiasi punto della circonferenza;- corda, un segmento che unisce due punti qualsiasi della circonferenza;
- diametro, qualsiasi corda che passi per il centro della circonferenza;
- arco, parte della circonferenza che unisce due punti sulla circonferenza;
- semicirconferenza, metà della circonferenza.

Se incliniamo la torcia in una direzione o nell’altra quindi a destra o a sinistra, il cono luminoso si deformerà, il cerchio di luce inizierà ad allungarsi definendo una nuova forma curva, una seconda conica che chiamiamo ellisse. In questo caso, immaginiamo di tagliare un cono con un piano leggermente inclinato rispetto al proprio asse (v. immagine a sinistra).
DEFINIZIONE:
“si definisce ellisse, il luogo geometrico dei punti di un piano per i quali è costante la somma delle distanze da due punti fissi detti fuochi“.
Gli elementi importanti che definiscono una ellisse, sono:
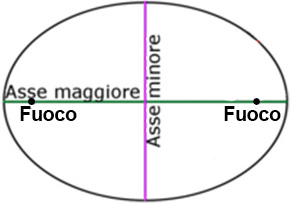 assi dell’ellisse, sono i segmenti che consentono di dividere l’ellisse in parti uguali;
assi dell’ellisse, sono i segmenti che consentono di dividere l’ellisse in parti uguali;- vertici, sono i 4 punti di intersezione tra l’ellisse e i suoi assi;
- centro, è l’intersezione degli assi e costituisce anche il centro di simmetria;
- fuochi, sono due punti che si trovano sempre sull’asse maggiore e sono posizionati in modo da essere equidistanti dal centro. Inoltre, per definizione sono quei due punti tali per cui la somma delle loro due distanze da ciascun punto appartenente all’ellisse è costante.

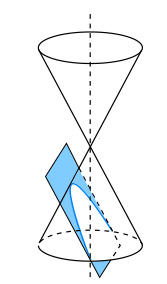
Se incliniamo ancora di più la torcia fino a quando non si trovi parallela al muro, noteremo che il cono luminoso si deformerà ulteriormente e il cerchio di luce inizierà ad allungarsi all’infinito definendo una nuova forma curva che chiamiamo parabola. In questo caso, è come se tagliassimo un cono con un piano parallelo ad uno dei suoi lati (v. immagine a sinistra).
DEFINIZIONE:
“si definisce parabola, il luogo geometrico dei punti equidistanti da un punto fisso detto fuoco e da una retta detta direttrice“.
Gli elementi importanti che definiscono una parabola, sono:
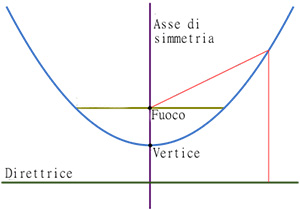 direttrice, è la retta, esterna o interna alla parabola, che realizza la stessa distanza rispetto al fuoco per ciascun punto della parabola;
direttrice, è la retta, esterna o interna alla parabola, che realizza la stessa distanza rispetto al fuoco per ciascun punto della parabola;- fuoco, è il punto che realizza la stessa distanza rispetto alla direttrice per ciascun punto della parabola;
- asse, è la retta passante per il fuoco che divide in due parti uguali la parabola, perpendicolare alla direttrice;
- vertice, è il punto di intersezione tra la parabola e l’asse di simmetria.

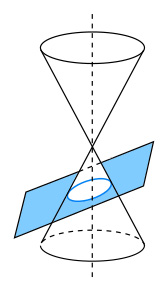
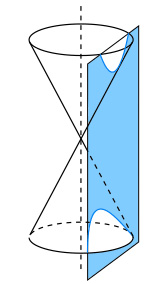 Se incliniamo la torcia fino a quando non si trovi in posizione parallela all’asse, il cono di luce cambierà ancora forma sdoppiandosi formando l’unica curva doppia nel cono a due falde che chiamiamo, iperbole. In questo caso il piano che taglia il cono a due falde è posizionato parallelamente all’asse (v. figura a sinistra).
Se incliniamo la torcia fino a quando non si trovi in posizione parallela all’asse, il cono di luce cambierà ancora forma sdoppiandosi formando l’unica curva doppia nel cono a due falde che chiamiamo, iperbole. In questo caso il piano che taglia il cono a due falde è posizionato parallelamente all’asse (v. figura a sinistra).
DEFINIZIONE:
“si definisce iperbole, il luogo geometrico dei punti per cui è costante la differenza delle distanze da 2 punti fissi detti fuochi“.
Gli elementi importanti che definiscono una iperbole, sono:
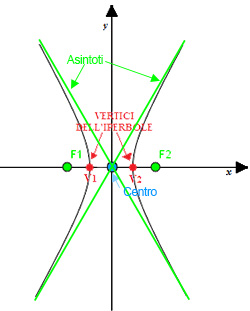 rami, le due curve che formano l’iperbole;
rami, le due curve che formano l’iperbole;- assi, sono le due rette per cui l’iperbole viene suddivisa in parti uguali e simmetriche; l’iperbole deve sempre intersecare uno dei due assi;
- vertici, sono i punti di intersezione tra i rami ed uno dei due assi;
- centro, è l’intersezione tra i due assi perpendicolari e rappresenta il centro di simmetria dell’iperbole;
- fuochi, sono i due punti fissi per i quali è costante la differenza tra le distanze da ogni punto appartenente all’iperbole e appartengono sempre all’asse che interseca l’iperbole;
- asintoti, sono le due rette passanti per il centro che racchiudono i due rami dell’iperbole.











 A questi strumenti se ne aggiunsero poi altri più complessi che consentirono di realizzare e disegnare curve ben più complesse delle rette o dei cerchi. La cosa interessante, nell’uso di questi strumenti non era tanto il risultato rappresentato sul supporto da disegno, bensì quello che consentivano lo spostamento di un punto lungo una direzione specifica, senza che il profilo di quest’ultima fosse materialmente presente.
A questi strumenti se ne aggiunsero poi altri più complessi che consentirono di realizzare e disegnare curve ben più complesse delle rette o dei cerchi. La cosa interessante, nell’uso di questi strumenti non era tanto il risultato rappresentato sul supporto da disegno, bensì quello che consentivano lo spostamento di un punto lungo una direzione specifica, senza che il profilo di quest’ultima fosse materialmente presente. Per comprendere quali curve è possibile ottenere, basta immaginare una parete di fronte a noi (il piano) colpita dal cono di luce prodotto da una torcia elettrica.
Per comprendere quali curve è possibile ottenere, basta immaginare una parete di fronte a noi (il piano) colpita dal cono di luce prodotto da una torcia elettrica.

 Se puntiamo una torcia perpendicolarmente ad una parete, il suo cono luminoso genererà su di essa una luce esattamente circolare, quindi definirà una curva che chiamiamo circonferenza. E’ come se tagliassimo un cono (v. immagine a sinistra) con un piano orizzontale perpendicolare al suo asse.
Se puntiamo una torcia perpendicolarmente ad una parete, il suo cono luminoso genererà su di essa una luce esattamente circolare, quindi definirà una curva che chiamiamo circonferenza. E’ come se tagliassimo un cono (v. immagine a sinistra) con un piano orizzontale perpendicolare al suo asse. raggio, il segmento che unisce il centro della circonferenza con qualsiasi punto della circonferenza;
raggio, il segmento che unisce il centro della circonferenza con qualsiasi punto della circonferenza;

 assi dell’ellisse, sono i segmenti che consentono di dividere l’ellisse in parti uguali;
assi dell’ellisse, sono i segmenti che consentono di dividere l’ellisse in parti uguali;

 direttrice, è la retta, esterna o interna alla parabola, che realizza la stessa distanza rispetto al fuoco per ciascun punto della parabola;
direttrice, è la retta, esterna o interna alla parabola, che realizza la stessa distanza rispetto al fuoco per ciascun punto della parabola;
 Se incliniamo la torcia fino a quando non si trovi in posizione parallela all’asse, il cono di luce cambierà ancora forma sdoppiandosi formando l’unica curva doppia nel cono a due falde che chiamiamo, iperbole. In questo caso il piano che taglia il cono a due falde è posizionato parallelamente all’asse (v. figura a sinistra).
Se incliniamo la torcia fino a quando non si trovi in posizione parallela all’asse, il cono di luce cambierà ancora forma sdoppiandosi formando l’unica curva doppia nel cono a due falde che chiamiamo, iperbole. In questo caso il piano che taglia il cono a due falde è posizionato parallelamente all’asse (v. figura a sinistra). rami, le due curve che formano l’iperbole;
rami, le due curve che formano l’iperbole;