PROIEZIONI ORTOGONALI di un QUADRATO

 Disegno
Mar 072013
 
P.O. QUADRATO
Dati LATO QUADRATO = 7 cm
CONSEGNE:
1 P.O. QUADRATO PARALLELO AL PIANO ORIZZONTALE
2 P.O. QUADRATO PARALLELO AL PIANO VERTICALE
3 P.O. QUADRATO PARALLELO AL PIANO LATERALE
4 REALIZZA LE P.O. UTILIZZANDO IL CAD
STRUMENTI NECESSARI:
OPERAZIONI INIZIALI:

usando un foglio F4, posizionato in orizzontale, effettuiamo la sua squadratura secondo lo schema appreso (vedi SQUADRATURA).

In questa esercitazione, effettueremo le 3 Proiezioni Ortogonali di un quadrato di lato dato. Nella prima, il quadrato sarà posto parallelamente al Piano Orizzontale, nella seconda al Piano Verticale e nella terza al Piano Laterale. In ognuna di esse sarà fondamentale disegnare il quadrato al centro del piano a cui è parallelo.

FIGURA DI RIFERIMENTO:

P.O. QUADRATO // AL PIANO ORIZZONTALE
01 – Il quadrato posto parallelamente al Piano Orizzontale, ossia al piano che passa sotto i nostri piedi come il pavimento su cui camminiamo si trova nella posizione descritta sotto rispetto ai tre piani e proietta la sua superficie proprio sul Piano Orizzontale. Essendo una figura bidimensionale e non avendo per cui spessore, sugli altri due piani proietterà due linee di lunghezza pari al lato del quadrato.

01 – Quadrato parallelo al Piano Orizzontale

02 – Nell’immagine seguente, potete osservare le tre proiezioni del quadrato sui tre piani ortogonali.

02 – Proiezioni del quadrato di lato dato sui tre piani ortogonali

03 – Una volta che i 3 piani vengono ribaltati sul foglio da disegno trovandosi in posizione complanare, saremo in grado di disegnare le Proiezioni Ortogonali del quadrato sul foglio. Si dovrà partire dal quadrato sul Piano Orizzontale per poter poi determinare le proiezioni sui piani Verticale e Laterale che, come detto, saranno due segmenti di lunghezza pari al lato del quadrato.

03 – Proiezioni ortogonali di un Quadrato parallelo al Piano Orizzontale

TUTORIAL VIDEO:
  1. dividiamo l’area da disegno in quattro parti uguali tracciando un asse orizzontale e uno verticale;
  2. trascriviamo con il normografo i nomi dei diversi piani: P.O. (Piano Orizzontale), P.V. (Piano Verticale), P.L. (piano laterale);
  3. trascriviamo, inoltre, sull’asse orizzontale, all’inizio e alla fine le lettere L. e T. (Linea di Terra);
  4. costruiamo ora su P.O. il QUADRATO dato il lato utilizzando il metodo appreso precedentemente;
  5. nominiamo ogni vertice del quadrato ABCD;
  6. proiettiamo ciascuno spigolo ABCD ortogonalmente su P.V.;
  7. all’altezza indicata sui dati dell’esercitazione, tracciamo il segmento proiezione del quadrato ABCD sul Piano Verticale e inseriamo i nomi degli spigoli come in figura;
  8. proiettiamo ora ABCD su P.L.; per fare ciò dovremo proiettare gli spigoli del quadrato sull’asse verticale della costruzione. Poi puntando il compasso al centro degli assi ribaltiamo le proiezioni ABCD su L.T.;
  9. alziamo adesso le proiezioni all’altezza stabilita precedentemente (l’altezza su P.V. e su P.L. è la stessa) e colleghiamo le proiezioni su P.V. e su P.L.;
  10. per completare l’elaborato, rinforziamo solo le proiezioni del quadrato sui tre diversi piani (linee in rosso).

P.O. QUADRATO // AL PIANO VERTICALE
01 – Il quadrato posto parallelamente al Piano Verticale, ossia al piano posto di fronte a noi come una parete si trova nella posizione descritta sotto rispetto ai tre piani e proietta la sua superficie proprio sul Piano Verticale. Essendo una figura bidimensionale e non avendo per cui spessore, sugli altri due piani proietterà due linee di lunghezza pari al lato del quadrato.

01 – Quadrato parallelo al Piano Verticale

02 – Nell’immagine seguente, potete osservare le tre proiezioni del quadrato sui tre piani ortogonali.

02 – Proiezioni del quadrato di lato dato sui tre piani ortogonali

03 – Una volta che i 3 piani vengono ribaltati sul foglio da disegno trovandosi in posizione complanare, saremo in grado di disegnare le Proiezioni Ortogonali del quadrato sul foglio. Si dovrà partire dal quadrato sul Piano Verticale per poter poi determinare le proiezioni sui piani orizzontale e laterale che, come detto, saranno due segmenti di lunghezza pari al lato del quadrato.

03 – Proiezioni ortogonali di un Quadrato parallelo al Piano Verticale

P.O. QUADRATO // AL PIANO LATERALE
01 – Il quadrato posto parallelamente al Piano Laterale, ossia al piano posto alla nostra destra come la parete di una stanza posta lateralmente a noi, si trova nella posizione descritta sotto rispetto ai tre piani e proietta la sua superficie proprio sul Piano Laterale. Essendo una figura bidimensionale e non avendo per cui spessore, sugli altri due piani proietterà due segmenti di lunghezza pari al lato del quadrato.

01 – Quadrato parallelo al Piano Laterale

02 – Nell’immagine seguente, potete osservare le tre proiezioni del quadrato sui tre piani ortogonali.

02 – Proiezioni del quadrato di lato dato sui tre piani ortogonali

03 – Una volta che i 3 piani vengono ribaltati sul foglio da disegno trovandosi in posizione complanare, saremo in grado di disegnare le Proiezioni Ortogonali del quadrato sul foglio. Si dovrà partire dal quadrato sul Piano Laterale per poter poi determinare le proiezioni sui piani Orizzontale e Verticale che, come detto, saranno due segmenti di lunghezza pari al lato del quadrato.

03 – Proiezioni ortogonali di un Quadrato parallelo al Piano Laterale

ESERCIZI CORRELATI:
ALTRI TUTORIAL:

ASSONOMETRIA: IL RIBALTAMENTO

 Didattica, Disegno
Feb 262013
 

Assonometria

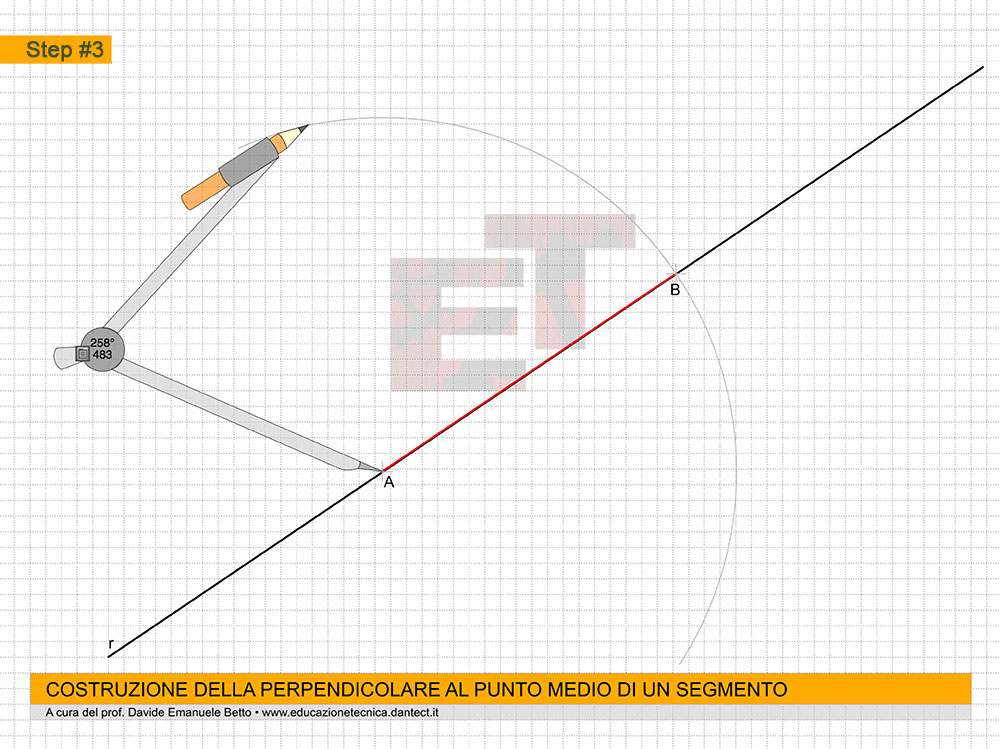
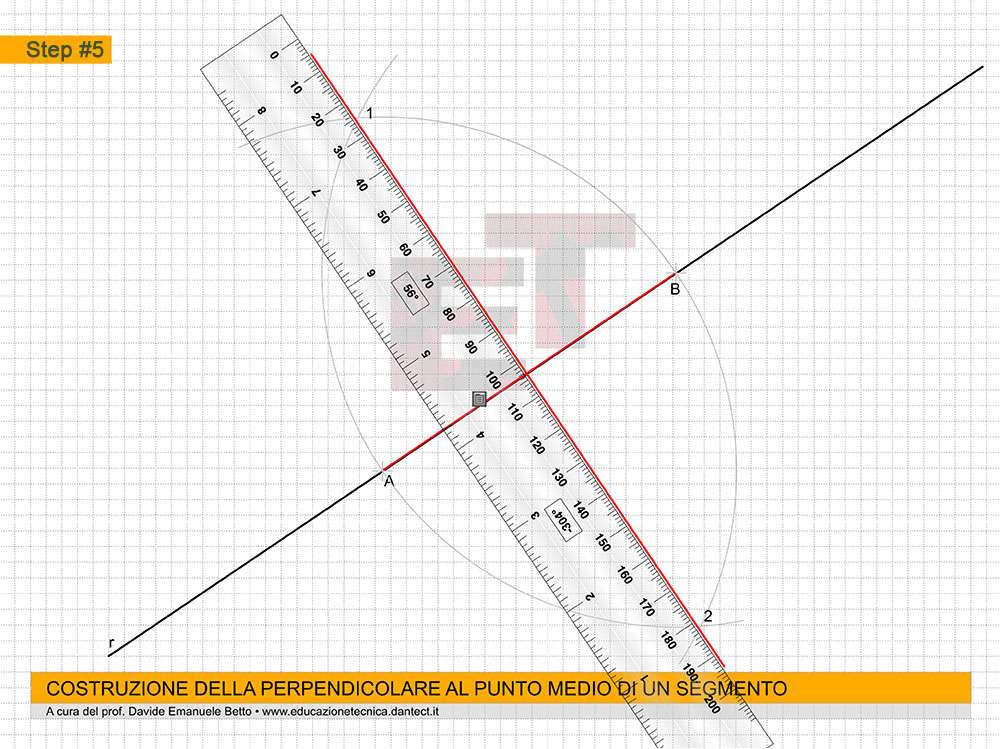
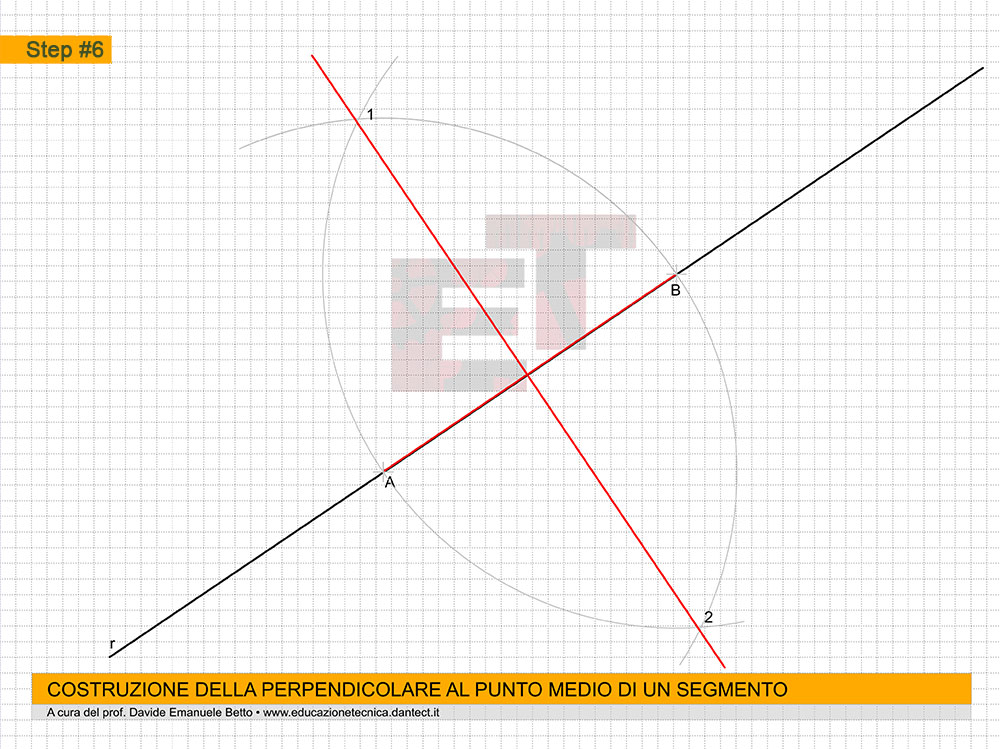
Questo capitolo si configura come un completamento di quello sulle ASSONOMETRIE.

PIRAMIDE4
PIRAMIDE QUADRATA CUBO

Fino a qui, abbiamo disegnato figure a base quadrangolare (parallelepipedo, cubo, piramidi a base rettangolare o quadrata), quindi relativamente semplici perché i loro lati di base sono sempre paralleli agli assi XY di riferimento (piano orizzontale) per cui di facilmente tracciabili.

I problemi nascono quando dobbiamo realizzare figure i cui lati non sono più paralleli agli assi  X e Y o quando ruotiamo la figura rispetto a questi. Ad esempio come per le figure con basi poligonali illustrate qui sotto:

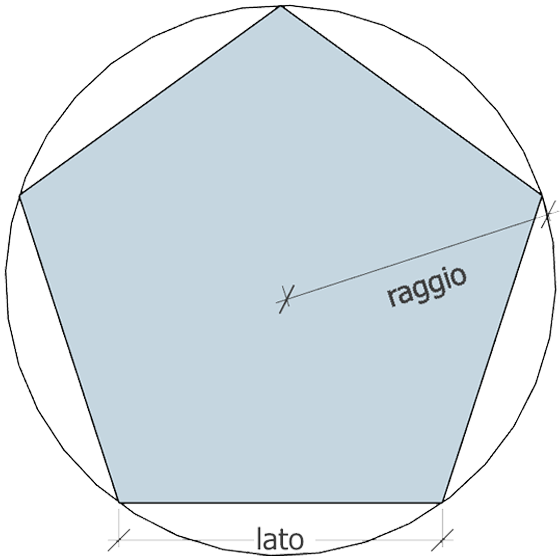
TETRAEDRO PIRAMIDE PENTAGONALE

In questi casi le proiezioni ortogonali ci vengono in aiuto. Infatti, unendo le due tecniche, riusciamo con facilità a realizzare qualunque figura geometrica in assonometria. In realtà il problema si pone principalmente nelle assonometrie Isometrica e Cavaliera in quanto nella Monometrica, il piano XY è ortogonale, quindi la figura di base può essere costruita con facilità sullo stesso.

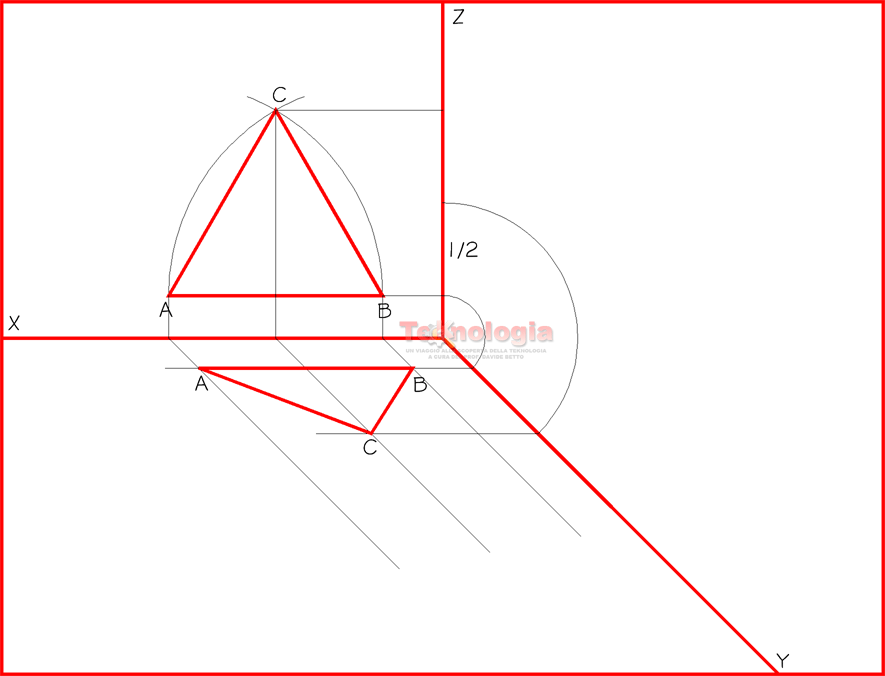
PRISMA3misureTracciati gli assi XYZ nella proiezione isometrica, cioè inclinati con un angolo di 120° tra di loro, tracciamo ora, un nuovo asse Y’ ortogonale a Z. Avremo così un nuovo piano virtuale denominato ZY’. La caratteristica di questo piano è quella che i due assi sono tra di loro perpendicolari. Su questo nuovo piano, andremo a costruire la base del nostro solido come se fossimo sul Piano Orizzontale delle Proiezioni Ortogonali.

Proviamo a realizzare l’assonometria isometrica di un PRISMA a base triangolare.

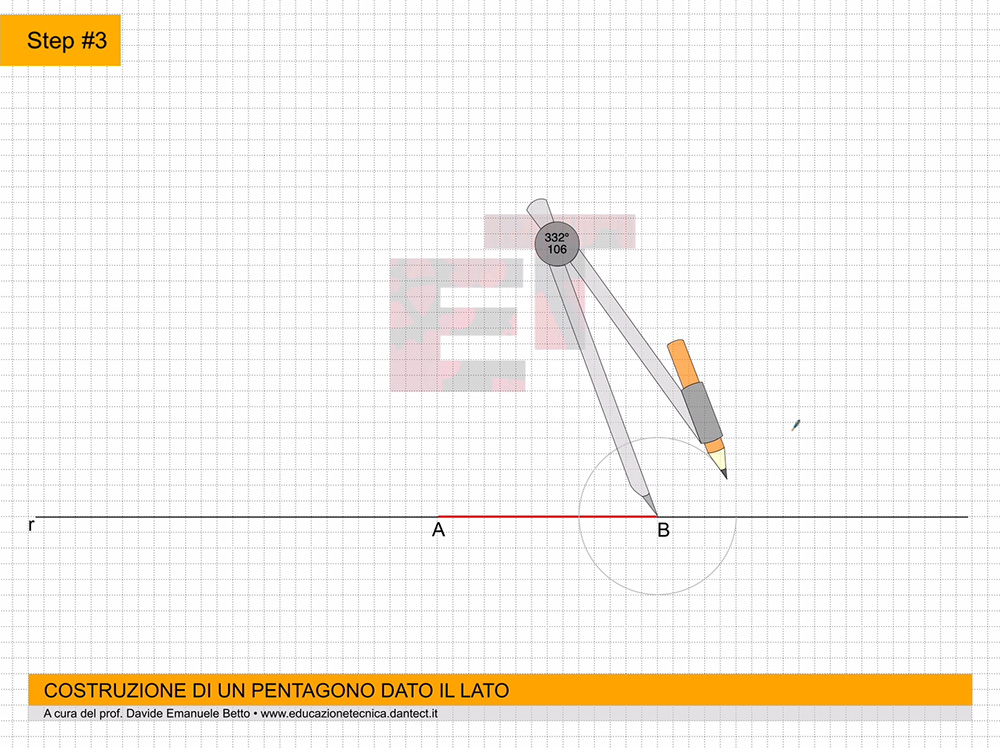
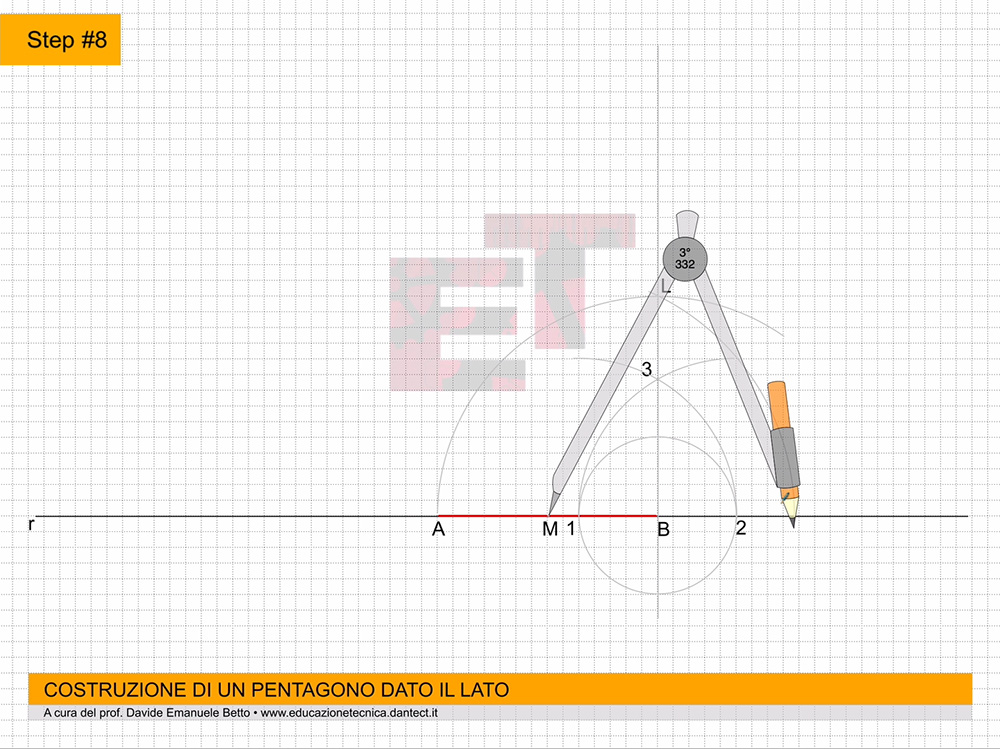
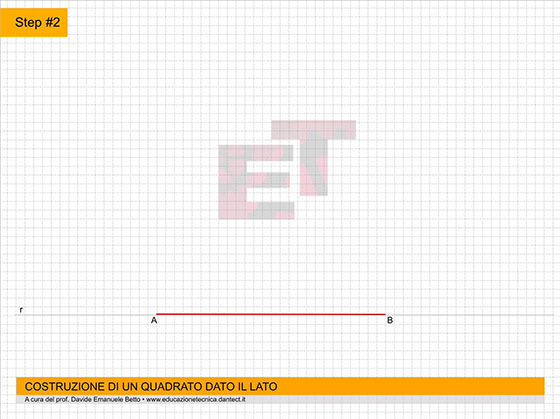
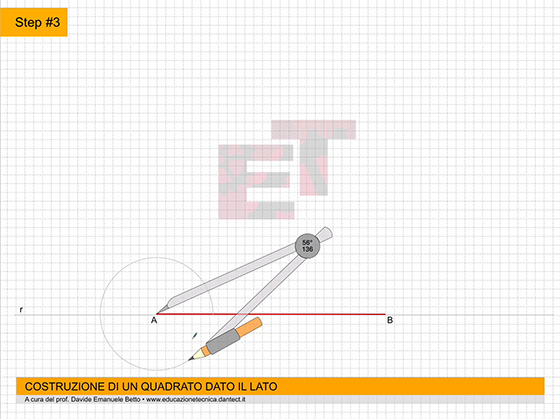
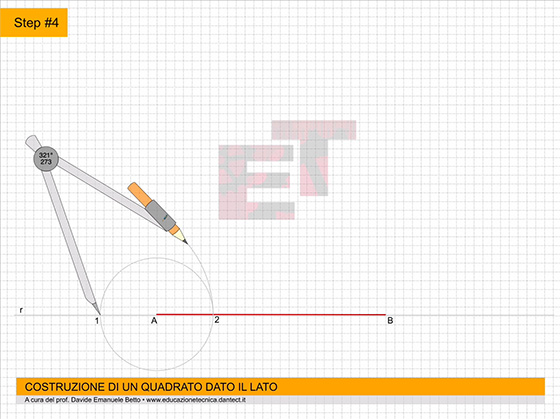
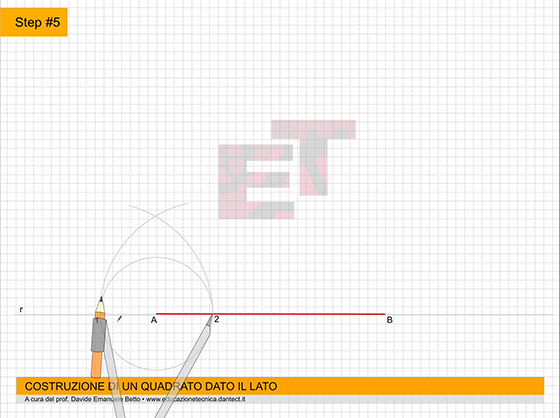
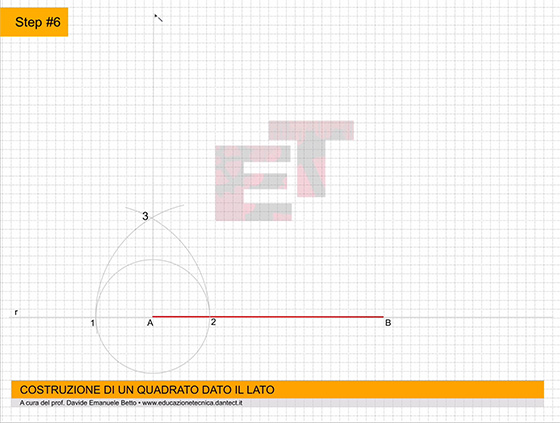
Procediamo con la costruzione; l’animazione di seguito ci può aiutare a comprendere il procedimento di costruzione del solido geometrico in oggetto.

Ribaltamento

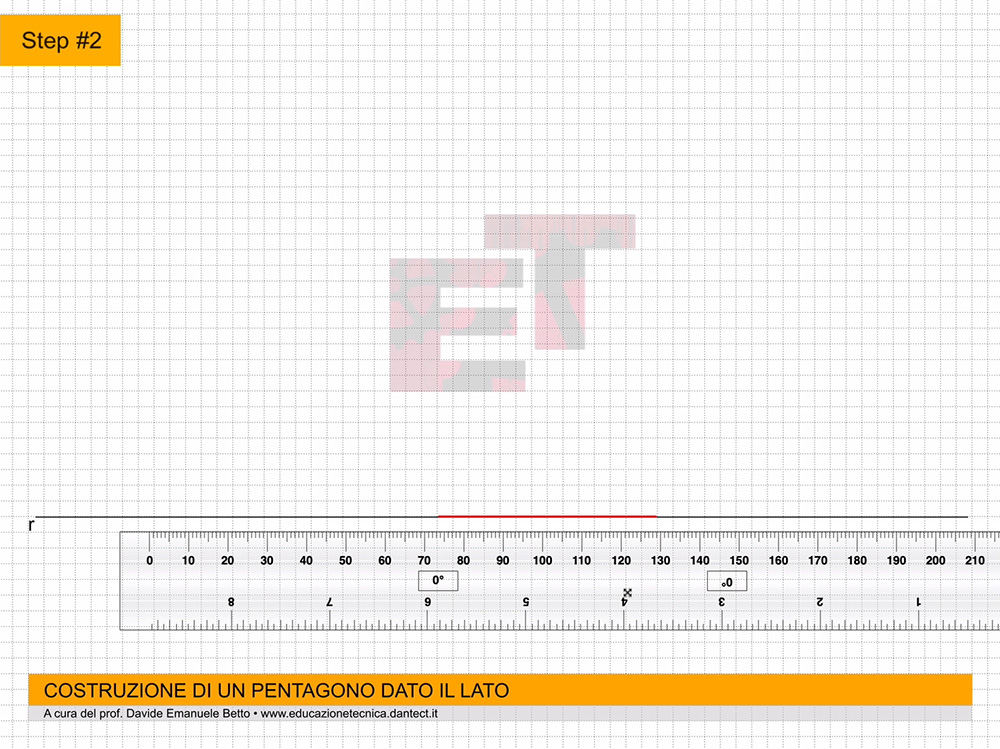
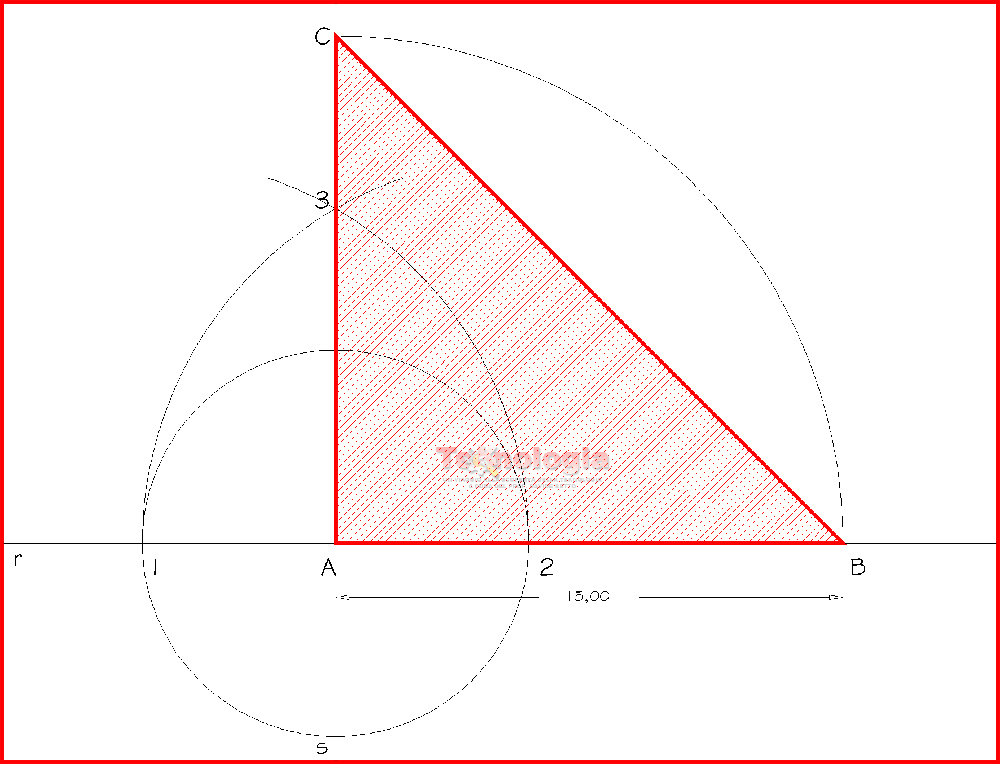
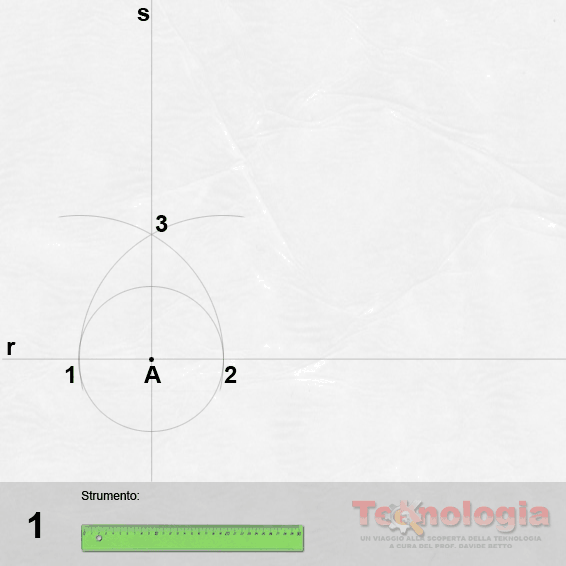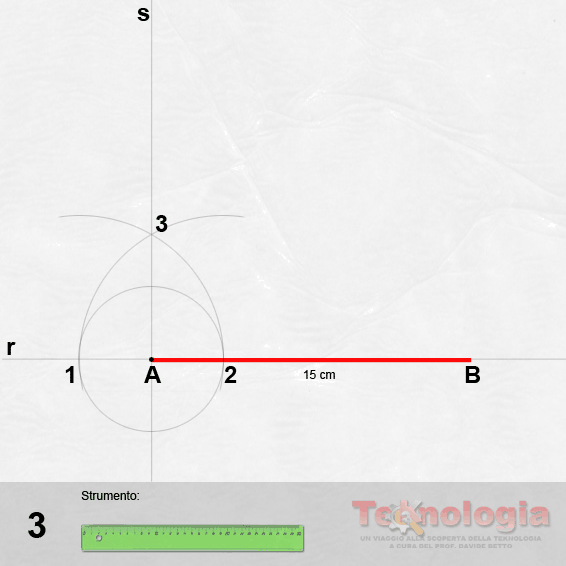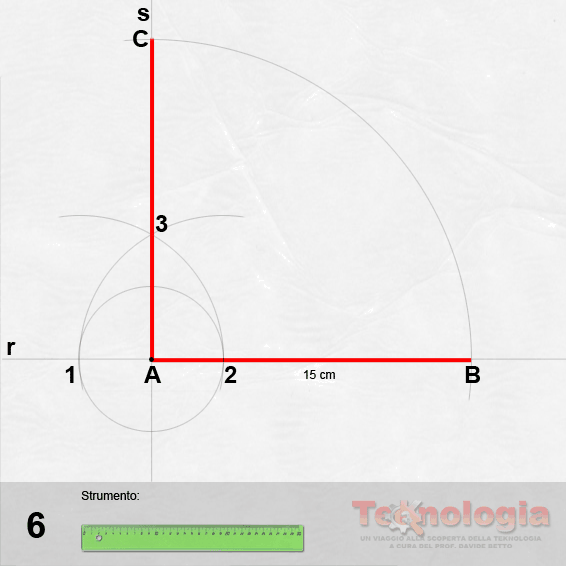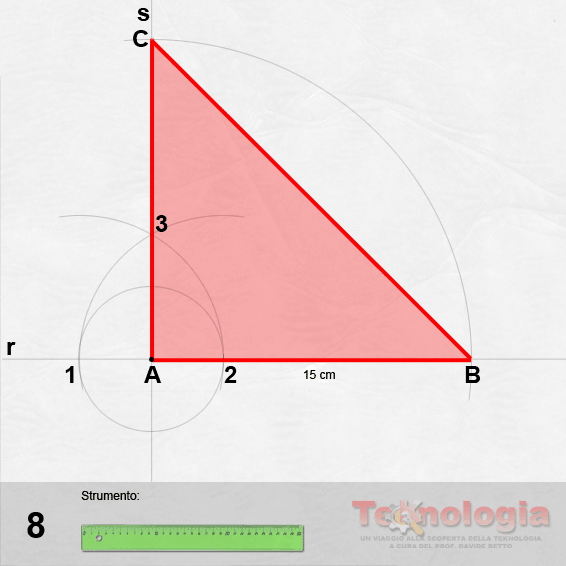
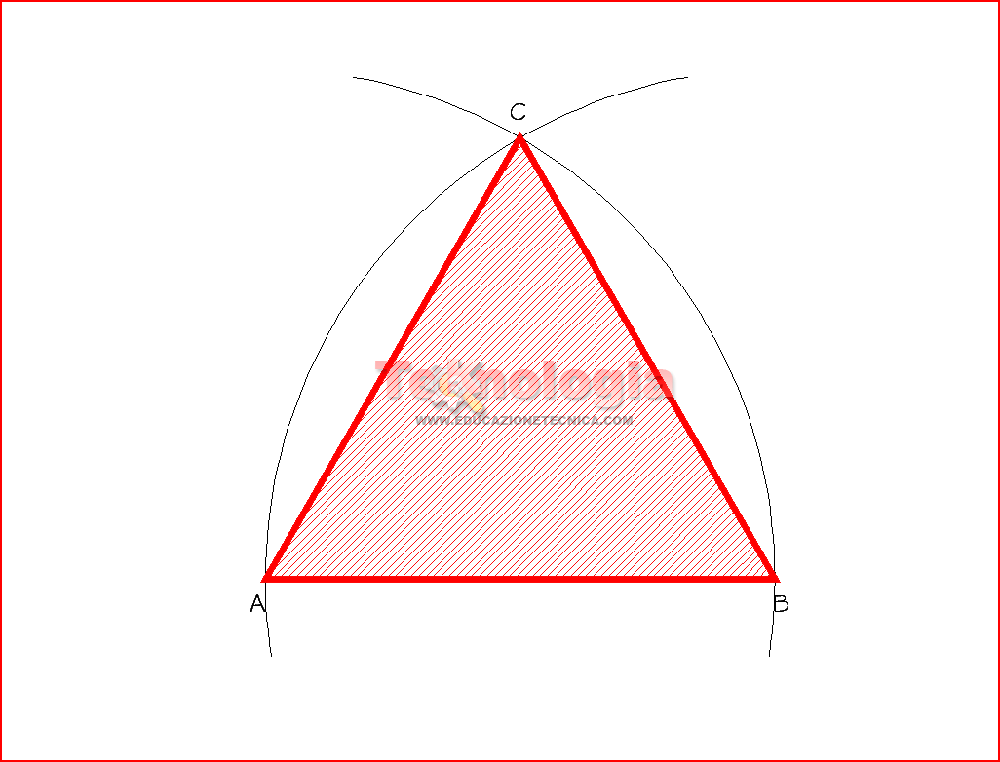
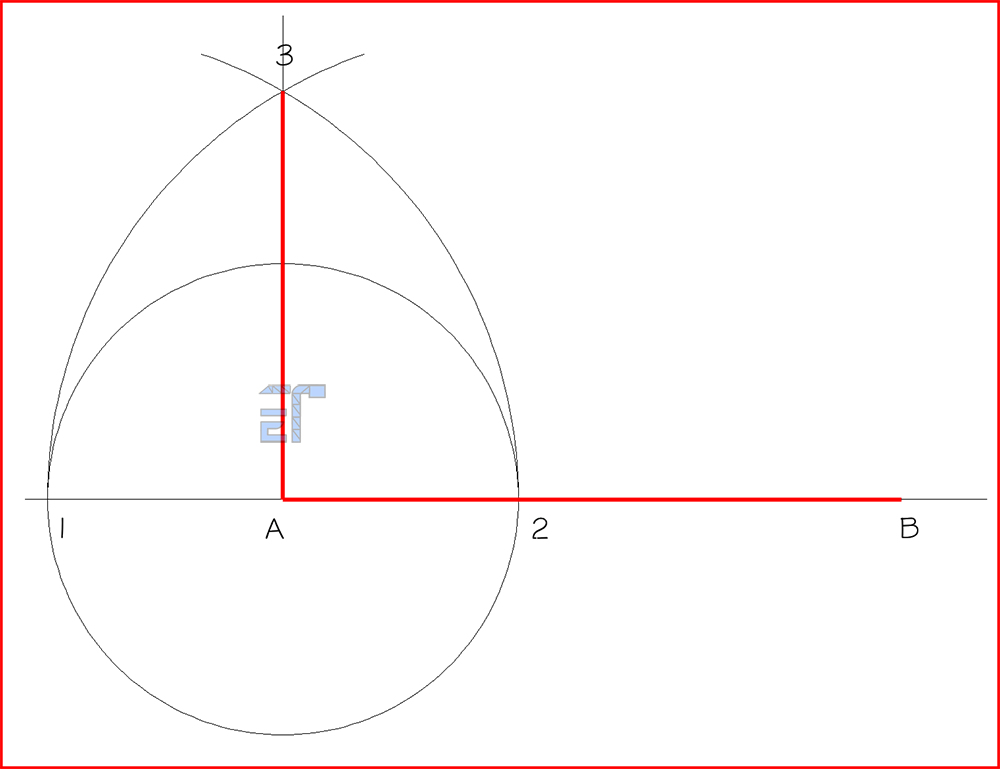
da 4 a 7 – Costruiamo il triangolo equilatero abc secondo il metodo già appreso.

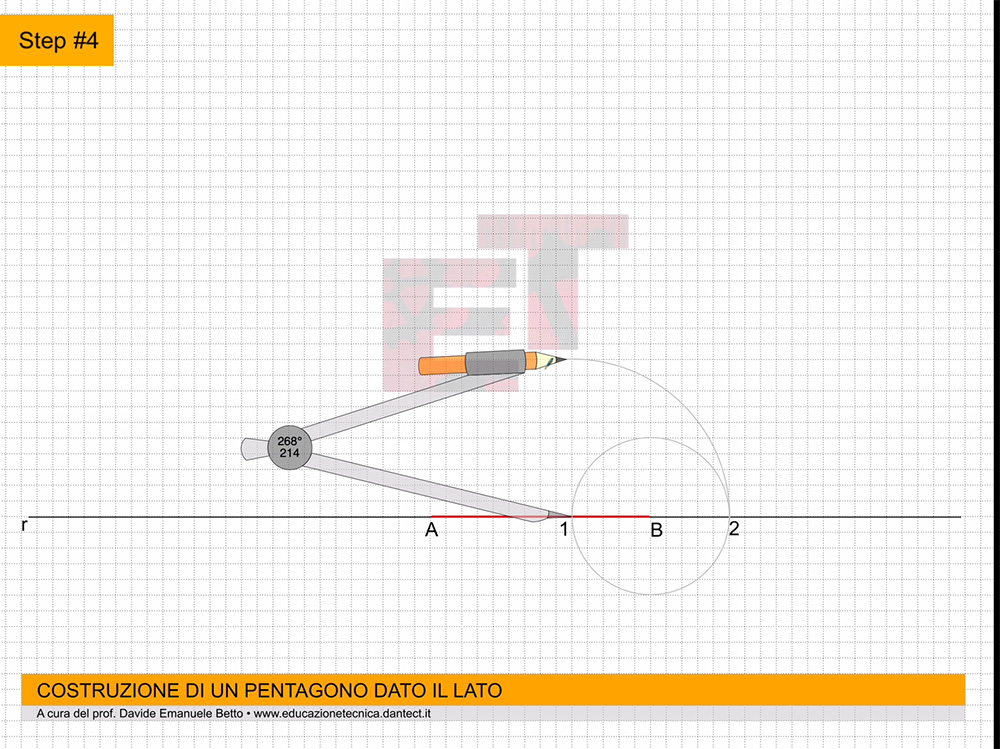
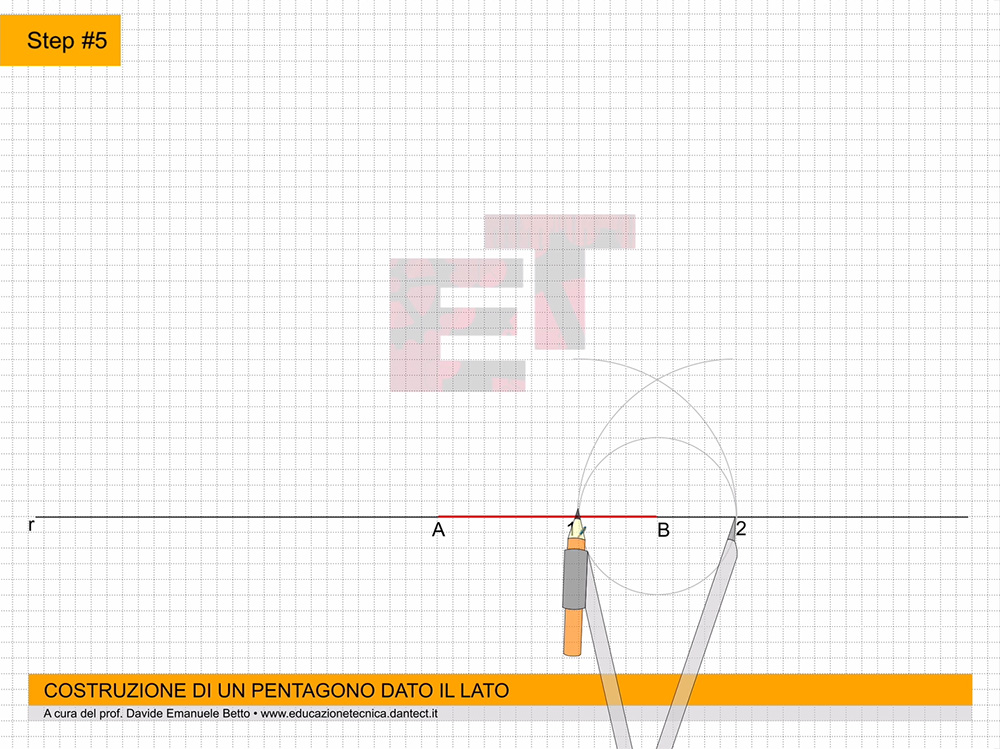
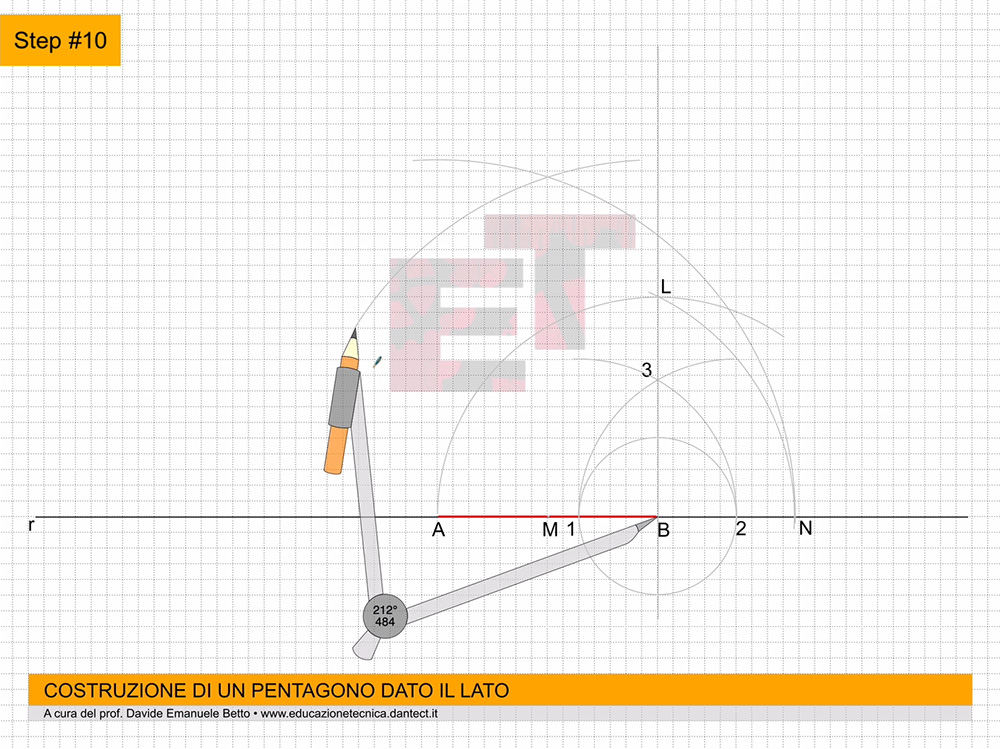
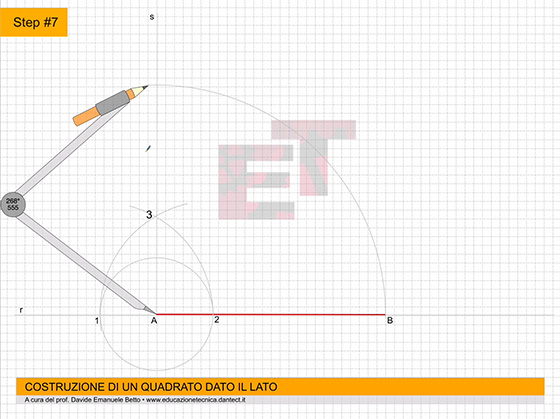
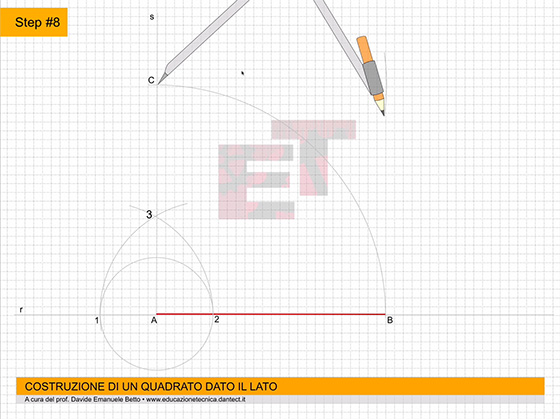
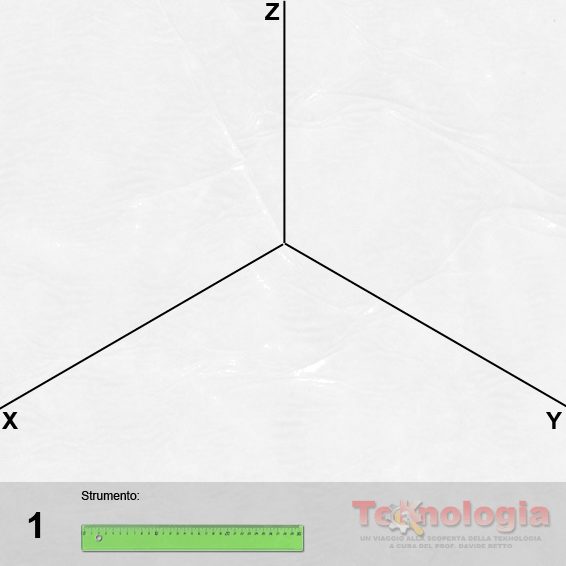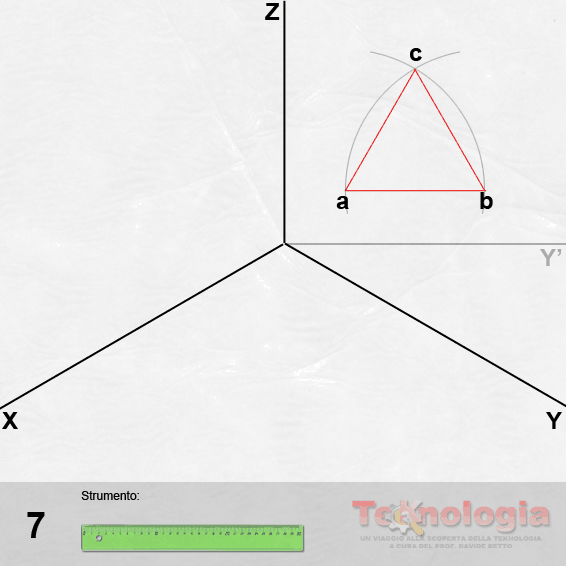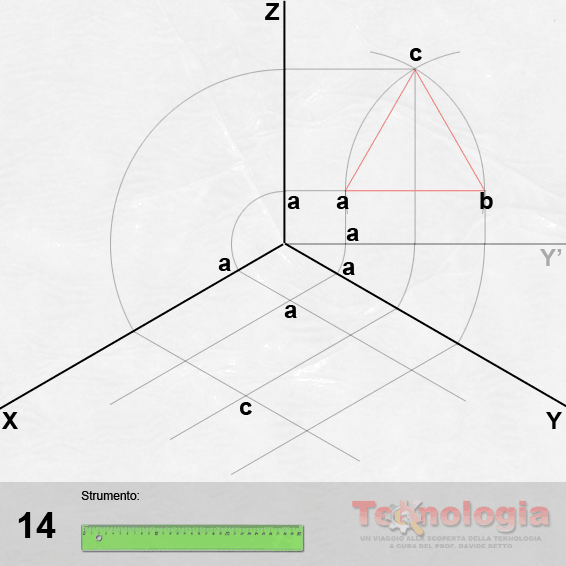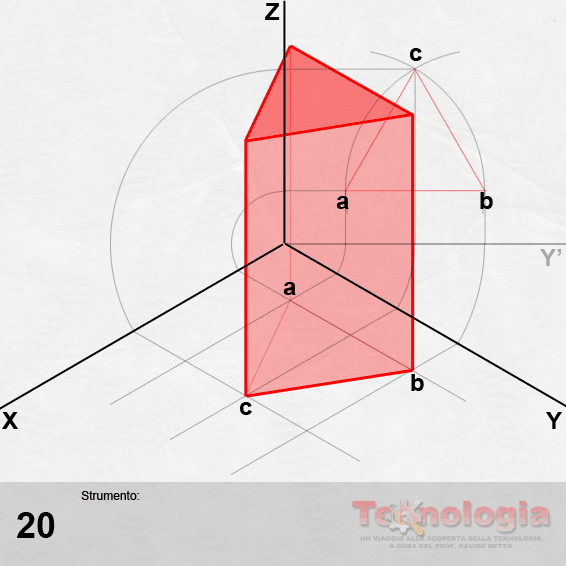
da 8 a 10 – Proiettiamo ciascun punto a, b, c, perpendicolarmente all’asse Z e di seguito, perpendicolarmente all’asse Y’. Adesso applichiamo il vero è proprio ribaltamento, cioè riportiamo sugli assi X e Y le proiezioni dei punti abc del triangolo di base del prisma. Per far ciò, puntiamo il compasso al centro degli assi, e con apertura oa, oc e ob, ruotiamo queste proiezioni da Y’ fino a toccare l’asse Y.

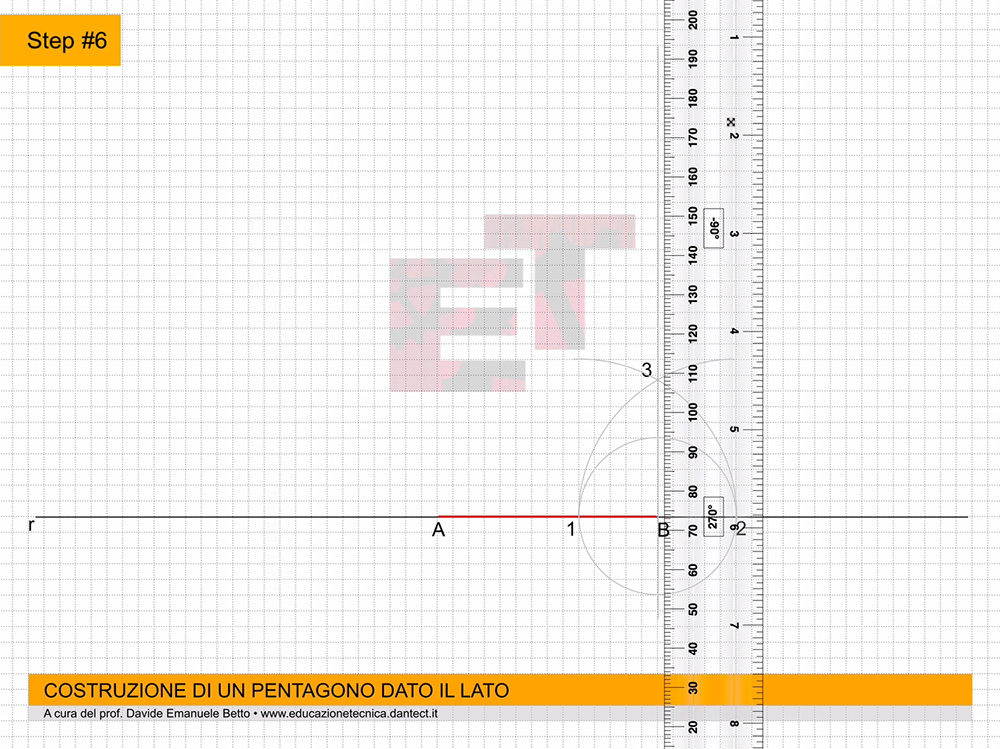
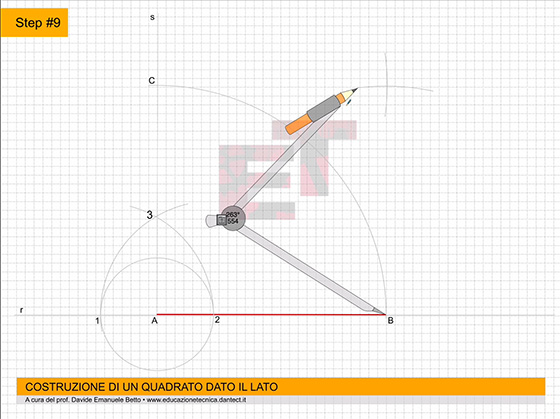
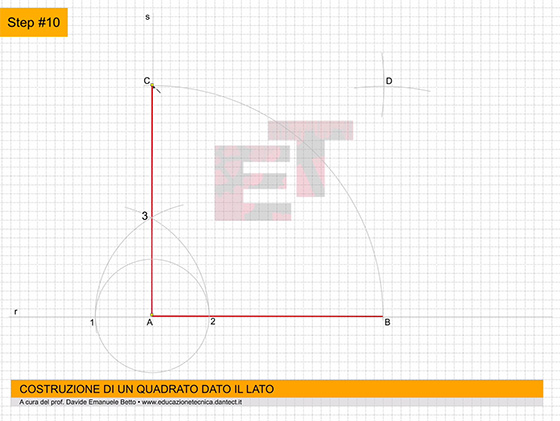
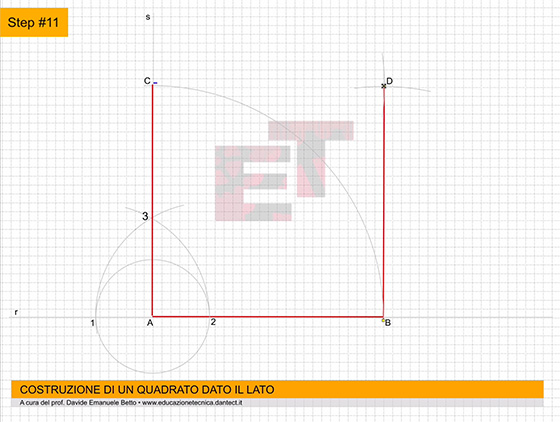
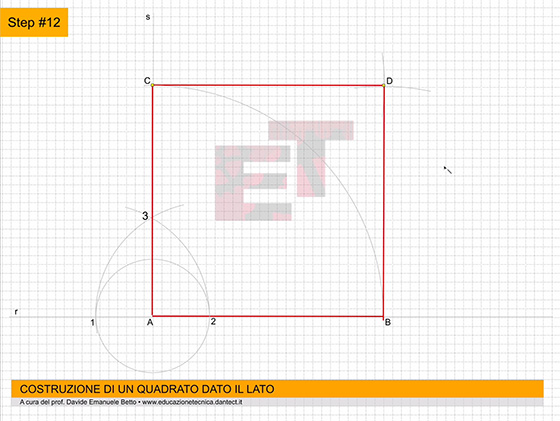
da 11 a 12 – Allo stesso modo, sempre puntando il compasso al centro degli assi, ruotiamo le proiezioni sull’asse Z fino a far toccare loro l’asse X. Ora, procedendo come abbiamo sempre fatto, proiettiamo questi punti parallelamente agli assi X e Y.

13 – Seguiamo le proiezioni di a sia sull’asse X che su quello Y e dal loro incrocio troveremo il punto a sul piano XY.

da 14 a 15 – Allo stesso modo, seguiamo le proiezioni di b e c sia su X che su Y, per trovare rispettivamente i punti a e b sul piano XY.

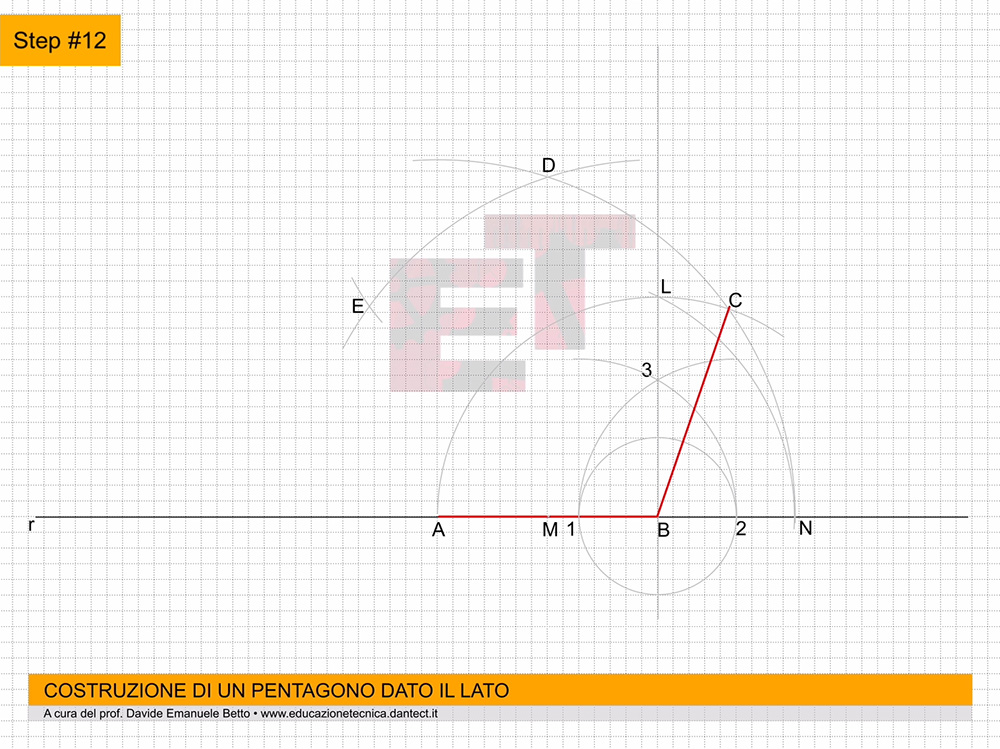
16 – Unendo i punti a, b e c sul piano XY, definiremo il triangolo di base inferiore del prisma triangolare.

17 – Alziamo da a, b e c le altezze per costruire la base superiore triangolare del prisma.

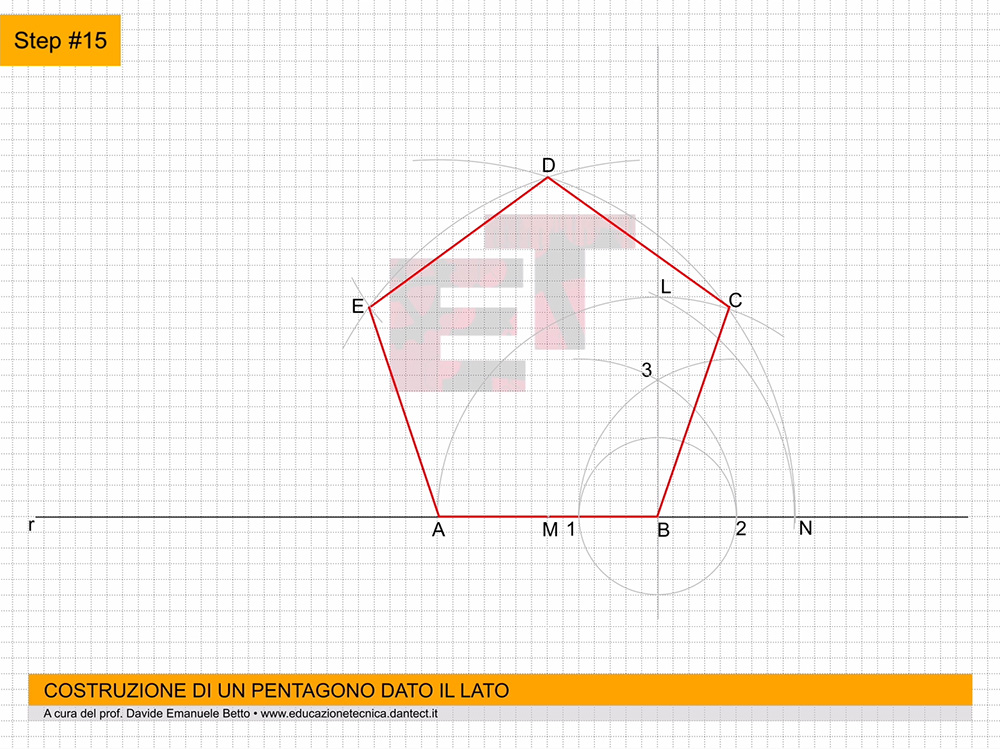
da 18 a 20 – Per completare la figura rinforziamo solo ciò che si vede.

ESEMPI

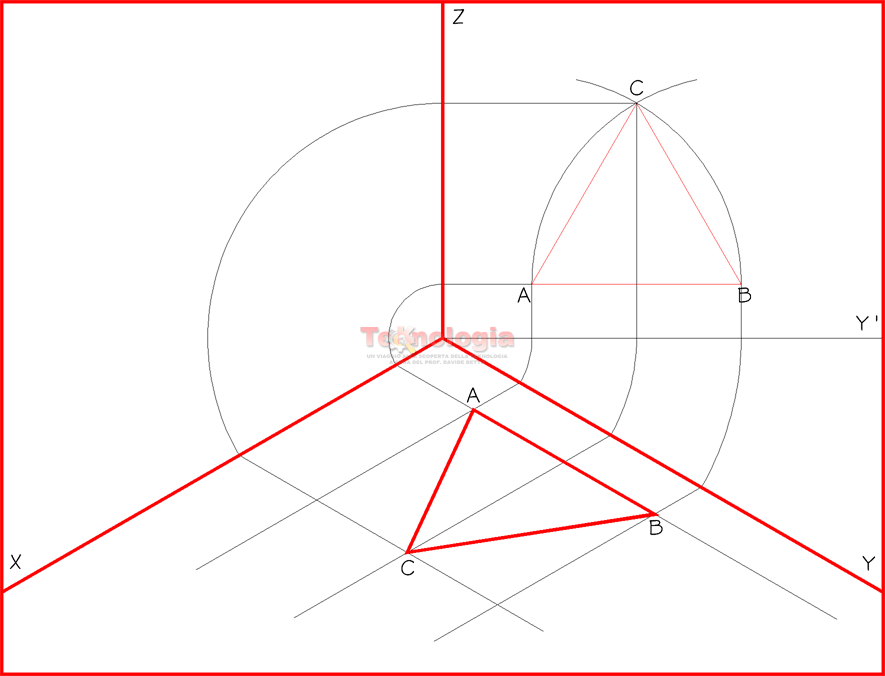
Di seguito vediamo un esempio di RIBALTAMENTO in ciascuno dei metodi assonometrici studiati:

ISOMETRICA

Nell’animazione precedente e nella descrizione è indicato passo passo la procedura per eseguirla:

RibaltamentoISO

MONOMETRICA

Nel caso dell’assonometria monometrica, come detto la figura geometrica di base può essere costruita direttamente sul piano XY (vedi Figura a), oppure utilizzare anche in questo caso il RIBALTAMENTO (vedi Figura b):

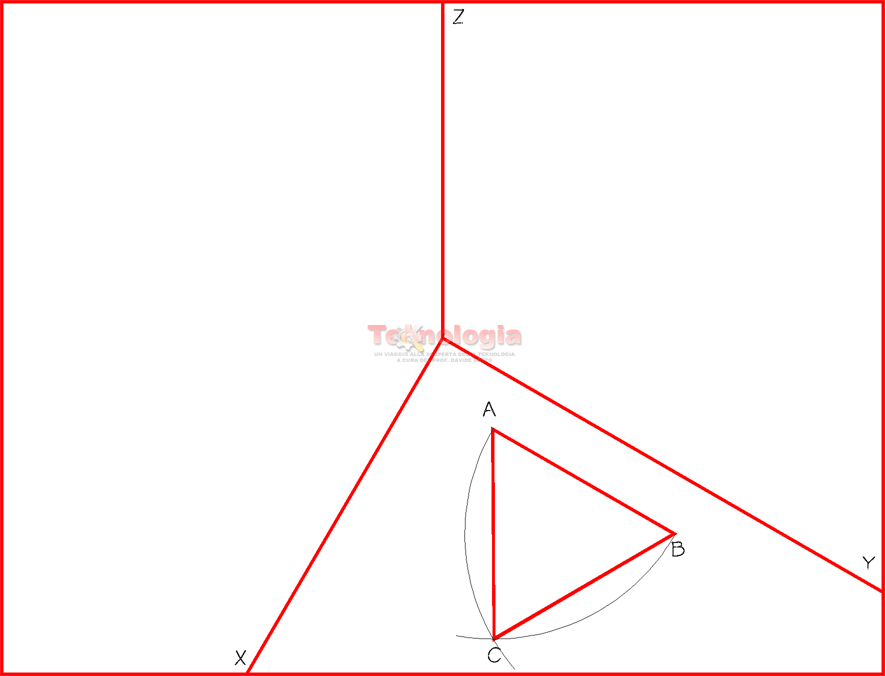
Costruzione diretta

a – Costruzione diretta

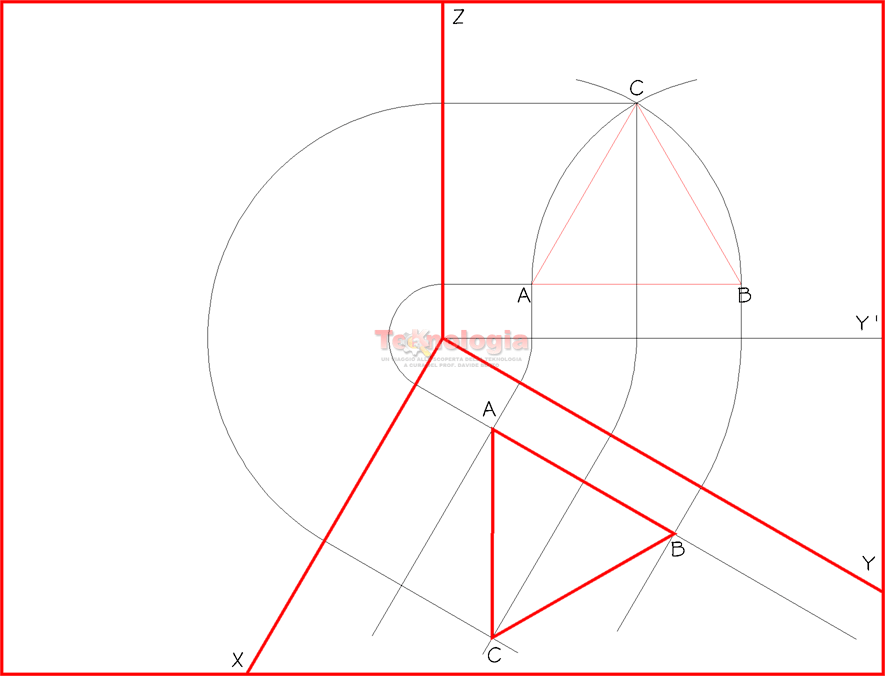
Costruzione con ribaltamento

b – Costruzione con ribaltamento

 

 

 

 

 

 

CAVALIERA

Nel caso dell’assonometria cavaliera, il piano virtuale ZY’ può essere il piano ZX già esistente perché ortogonale. In questo caso, l’unica accortezza è quella di ricordarsi di dimezzare le misure della proiezione su Y come da tecnica costruttiva:

RibaltamentoCAV

PUOI LEGGERE ANCHE:

METODO GENERALE: PENTAGONO

 Disegno
Feb 162013
 

Il METODO GENERALE, è una procedura grafica con la quale è possibile disegnare qualunque poligono regolare, utilizzando lo stesso metodo. Non è possibile definire in questo caso la dimensione del lato del poligono, bensì si dovrà partire dal diametro del cerchio che inscrive il poligono da disegnare.

Per rendere più semplice la procedura, sarà opportuno, fare in modo che il diametro del cerchio, sia sempre un multiplo del numero dei lati del poligono da disegnare. Quindi, ad esempio, se dobbiamo disegnare un pentagono, ossia un poligono di 5 lati, la dimensione del cerchio che lo inscrive dovrà essere un multiplo di questi lati, ossia misurare 10, 15, 20,…. cm, perché in questo modo sarà più facile poterlo dividere secondo il procedimento grafico. Se il poligono è un esagono (6 lati), il diametro del cerchio potrà essere 12,18,….cm. Stessa procedura per l’ettagono, ottagono, ecc.

ESEMPIO: COSTRUZIONE DI UN PENTAGONO

DESCRIZIONE:

Strumenti da Disegno: foglio F4 liscio gr.220, matita HB/2, squadrette, riga e compasso.

Livello: classi seconde.

Difficoltà: media.

Descrizione: usando un foglio dall’album da disegno, effettuiamo la squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare l’esercitazione della scheda sopra.

PROCEDURA OPERATIVA:

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

  1. dividere con due rette una orizzontale r e una verticale s il foglio in 4 parti uguali;
  2. puntiamo il compasso al centro del foglio, all’incrocio delle due linee r e s e tracciamo una circonferenza del diametro stabilito (10cm o 15cm) che intersecherà le due rette nei punti A e B su r e C e D su s;
  3. dividiamo ora il segmento CD in un numero di parti pari al numero di lati della figura che andremo a realizzare (stiamo costruendo un pentagono, per cui il segmento CD andrà diviso in 5 parti uguali);
  4. puntiamo il compasso in C e con apertura CD (pari al diametro dl cerchio), tracciamo un arco di circonferenza che intersecherà la retta orizzontale r in un punto E;
  5. uniamo ora E con il punto 2 sul segmento CD (il punto 2 è il secondo tratto in cui abbiamo diviso CD) e prolunghiamo questa retta fino ad incontrare la circonferenza nel punto F;
  6. la distanza DF rappresenta la lunghezza di uno dei lati del pentagono. Essendo il pentagono che andiamo a disegnare una figura regolare, ossia con lati e angoli tutti uguali, apriamo il compasso con lunghezza DF e puntandolo su F tracciamo un archetto che interseca la circonferenza in un punto G;
  7. puntiamo ora il compasso in D con la stessa apertura DF e tracciamo un archetto che interseca la circonferenza in un punto H;
  8. infine, puntiamo il compasso su H sempre con la stessa apertura (DF) e tracciamo un archetto che interseca la circonferenza in un punto I;
  9. uniamo i punti DFGIH; otterremo il PENTAGONO costruito con il metodo detto generale.

MetGenPent_movie

SCARICA L’ARTICOLO:

COSTRUZIONE di un PENTAGONO dato il LATO

 Didattica, Disegno
Gen 312013
 
PENTAGONO DATO IL LATO
Dati Il LATO misura 8 cm o secondo indicazione del docente
CONSEGNE:
Consegna 1 Esegui la costruzione geometrica
Digit Esegui le consegne in digitale utilizzando il CAD
DIFFICOLTA’ e CLASSE:
Livello Classe
STRUMENTI NECESSARI:
DESCRIZIONE:

Prima di iniziare, pulisci il piano di lavoro e gli strumenti da disegno. Usando un foglio F4 liscio, effettua la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le consegne.

FIGURA DI RIFERIMENTO:

PROCEDURA OPERATIVA

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

Step #1 – tracciamo una retta orizzontale r nella parte bassa del foglio;

Step #2 – tracciamo poi un segmento A-B di lunghezza data al centro della retta r;

Step #3 – punta il compasso in B e con apertura a piacere, ma comunque inferiore alla metà di A-B, e traccia una circonferenza che intersecherà la retta r nei punti 1 e 2;

Step #4 – adesso con apertura 1-2, punta il compasso in 1 e traccia un arco di circonferenza dalla parte superiore della retta r;

Step #5 – con la stessa apertura, punta il compasso in 2 e traccia l’arco opposto; i due archi si intersecheranno in un punto che chiameremo 3;

Step #6 – con il righello uniamo i punti B e 3 tracciando così la retta perpendicolare a r passante per B;

Step #7 – puntiamo il compasso in B e con apertura B-A pari alla lunghezza del segmento dato, tracciamo un arco di circonferenza che intersecherà la retta verticale in un punto che chiameremo L;

Step #8 – con il righello o la squadretta, misuriamo la metà del segmento A-B che indicheremo con la lettera M; puntiamo il compasso in M e con apertura M-L, tracciamo un arco che intersecherà la retta r in un punto N;

Step #9 – adesso puntiamo il compasso in A e con apertura A-N, tracciamo un arco dalla parte superiore della retta r sufficientemente lungo;

Step #10 – senza cambiare l’apertura puntiamo il compasso sul punto B e tracciamo l’arco opposto che intersecherà il precedente in un punto che chiameremo D;

Step #11 – apriamo adesso il compasso con la lunghezza A-B pari alla misura del lato dato e puntiamolo in D per tracciare un arco che intersecherà quello precedente in un punto che chiameremo E;

Step #12 / 15 – a questo punto possiamo disegnare il pentagono unendo il punto B con C, C con D, D con E ed infine E con A.

Ricordo che le linee colorate di rosso sono quelle che vanno rinforzate nel disegno.

TUTORIAL VIDEO

COSTRUZIONE di un PENTAGONO data la CIRCONFERENZA

 Didattica, Disegno
Gen 212013
 
PENTAGONO DATA LA CIRCONFERENZA
Dati RAGGIO CIRCONFERENZA 8 cm o secondo indicazione del docente
CONSEGNE:
Consegna 1 Esegui la costruzione geometrica
Digit Esegui le consegne in digitale utilizzando il CAD
DIFFICOLTA’ e CLASSE:
Livello Classe
STRUMENTI NECESSARI:
DESCRIZIONE:

Prima di iniziare, pulisci il piano di lavoro e gli strumenti da disegno. Usando un foglio F4 liscio, effettua la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le consegne.

FIGURA DI RIFERIMENTO:

PROCEDURA OPERATIVA

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

STEP #01 – con la riga o la squadretta tracciamo gli assi orizzontale e verticale r e s che si intersecano in O passanti per il centro del foglio;

STEP #02 – puntiamo il compasso in O e con apertura data, pari al raggio della circonferenza, tracciamo un cerchio che interseca l’asse r nei punti A e B e l’asse s nei punti C e D;

STEP #03 – con il righello determiniamo il punto medio tra O e B che chiameremo M;

STEP #04 – puntiamo il compasso in M e con apertura MC, tracciamo un arco che interseca l’asse r in un punto che chiameremo N;

STEP #05 – puntiamo poi il compasso in D e con apertura DN, tracciamo un altro arco che intersecherà la circonferenza nei punti E ed F;

STEP #06 – senza cambiare l’apertura, puntiamo il compasso in E e tracciamo un archetto che interseca la circonferenza in un punto che chiameremo G. Allo stesso modo puntiamo il compasso in F e tracciamo un altro archetto che intersecherà la circonferenza in un punto che chiameremo H;

STEP #07 – a questo punto con il righello uniamo il punto D con il punto E; allo stesso modo uniamo E con G, G con H, H con F e infine F con D.

Ricordo che le linee colorate di rosso sono quelle che vanno rinforzate nel disegno.

VIDEO

COSTRUZIONE di un TRIANGOLO RETTANGOLO SCALENO

 Disegno
Dic 102012
 

DESCRIZIONE:

Strumenti da Disegno: foglio F4 liscio gr.220, matita HB/2, squadrette, riga e compasso.

Livello: classi seconde.

Difficoltà: bassa.

Descrizione: usando un foglio dall’album da disegno, effettuiamo la squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le esercitazioni della scheda sopra.

PROEDURAOPERATIVA:

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

  1. partiamo da quanto realizzato nella tavola n.2 ossia nell’esercizio per la costruzione della PERPENDICOLARE all’ESTREMO di un SEGMENTO;
  2. con il compasso, con apertura 12 cm, tracciamo sella retta r il segmento AB;
  3. sempre con il compasso, con apertura 15 cm, tracciamo sulla retta s il segmento AC;
  4. uniamo B e C, otterremo un triangolo rettangolo scaleno in quanto tutti e tre i lati sono tra loro diversi.

SCARICA L’ARTICOLO:

 

COSTRUZIONE di un TRIANGOLO RETTANGOLO ISOSCELE

 Disegno
Dic 102012
 

DESCRIZIONE:

Strumenti da Disegno: foglio F4 liscio gr.220, matita HB/2, squadrette, riga e compasso.

Livello: classi seconde.

Difficoltà: media.

Descrizione: usando un foglio dall’album da disegno, effettuiamo la squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le esercitazioni della scheda sopra.

PROCEDURA OPERATIVA:

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

  1. partiamo da quanto realizzato nella tavola n.2 ossia nell’esercizio per la costruzione della PERPENDICOLARE all’ESTREMO di un SEGMENTO;
  2. misuriamo sulla retta r a partire da A, una lunghezza di 15 cm;
  3. tracciamo su r il segmento AB di tale lunghezza;
  4. puntando il compasso in A, con apertura AB, tracciamo un arco che interseca sia la retta r che la retta s nei rispettivi punti B e C;
  5. uniamo B e C, otterremo un triangolo rettangolo isoscele in quanto due lati AB e AC sono tra loro uguali.

LINEE INCROCIATE

 Didattica, Disegno
Nov 212012
 
LINEE INCROCIATE
Dati LINEE INCLINATE a destra e sinistra distanti 2 quadretti e poi 1 quadretto
CONSEGNE:
Consegna 1 LINEE INCROCIATE 1
Consegna 2 LINEE INCROCIATE 2
Digit Esegui le consegne in digitale utilizzando il CAD
DIFFICOLTA’ e CLASSE:
Livello Classe
STRUMENTI NECESSARI:
DESCRIZIONE:

usando un foglio a quadri dal quadernone, effettuiamo la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le 2 consegne delle schede sotto.

LINEE INCROCIATE 1

posizionando il foglio in verticale (ossia con il lato corto verso di noi) e i fori a sinistra, procediamo nel seguente modo:

è importante notare come queste schede di disegno siano un’evoluzione di un’altra scheda, quella sulle linee inclinate. Per cui bisognerà procedere nel seguente modo:

  • quindi procedere allo stesso modo, ma tracciando le linee nella direzione opposta;

  • otterrete così una griglia di linee perpendicolari tra di loro ma inclinate di 45°.

LINEE INCROCIATE 2

Ripeti la stessa procedura distanziando, questa volta, le linee solo di 1 quadratino. Otterrai una sequenza con il doppio delle linee rispetto alla consegna precedente.

  • procedere come per l’esercizio precedente fino ad aver riempito tutta l’area da disegno.

LINEE INCLINATE

 Didattica, Disegno
Nov 162012
 
LINEE INCLINATE
Dati LINEE INCLINATE distanti 2 quadretti e poi 1 quadretto
CONSEGNE:
Consegna 1 LINEE INCLINATE 1
Consegna 2 LINEE INCLINATE 2
Digit Esegui le consegne in digitale utilizzando il CAD
DIFFICOLTA’ e CLASSE:
Livello Classe
STRUMENTI NECESSARI:
DESCRIZIONE:

usando un foglio a quadri dal quadernone, effettuiamo la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le 2 consegne delle schede sotto.

LINEE INCLINATE 1

posizionando il foglio in verticale (ossia con il lato corto verso di noi) e i fori a sinistra, procediamo nel seguente modo:

  • partendo dall’alto dell’area da disegno, segniamo con la matita ogni 2 quadretti verso destra un puntino di riferimento. E’ importante che vediate il puntino, ma che questo non sia eccessivamente grande e preponderante rispetto al disegno.
  • allo stesso modo, sempre dall’alto a sinistra e procedendo questa volta verso il basso, segniamo ogni 2 quadretti un puntino, per tutta la lunghezza della linea.
  • ripetiamo la stessa operazione sul lato destro della squadratura e sulla linea in basso, ossia per tutto il rettangolo di disegno.
  • avendo completato di segnare i puntini sui quattro lati dell’area da disegno, potremo cominciare a tracciare le linee inclinate del nostro disegno come in figura sotto.

  •  Completare tracciando le linee inclinate per tutta l’area da disegno.

LINEE INCLINATE 2

Ripeti la stessa procedura distanziando, questa volta, le linee solo di 1 quadratino. Otterrai una sequenza con il doppio delle linee rispetto alla consegna precedente.

  • procedere come per l’esercizio precedente fino ad aver riempito tutta l’area da disegno.

 

COSTRUZIONE di un TRIANGOLO EQUILATERO

 Disegno
Ott 292012
 

TriangoloEquilatero

DESCRIZIONE:

Strumenti da Disegno: foglio F4 liscio gr.220, matita HB/2, squadrette, riga e compasso.

Livello: classi seconde.

Difficoltà: bassa.

Descrizione: usando un foglio dall’album da disegno, effettuiamo la squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le esercitazioni della scheda sopra.

PROCEDURA OPERATIVA:

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

  1. tracciare una retta orizzontale r per tutta la lunghezza del foglio, avendo cura di tracciarla leggermente più in basso della metà foglio;
  2. individuare sulla retta r un segmento AB lungo 15 cm;
  3. adesso, puntando il compasso in A con apertura AB, tracciare un arco come in figura; analogamente puntare il compasso in B e con apertura BA tracciare l’archetto come in figura. I due archi si incontreranno in un punto che chiameremo C;
  4. basterà adesso unire il punto C con il punto A;
  5. infine, unire il punto C con il punto B per definire gli ultimi due lati del triangolo equilatero che sarà così costruito.

SCARICA L’ARTICOLO:

COSTRUZIONE di un QUADRATO dato il lato

 Didattica, Disegno
Ott 292012
 
QUADRATO DATO IL LATO
Dati LATO DEL QUADRATO pari a 12 cm o secondo indicazione del docente
CONSEGNE:
Consegna 1 Esegui la costruzione geometrica
Digit Esegui le consegne in digitale utilizzando il CAD
DIFFICOLTA’ e CLASSE:
Livello Classe
STRUMENTI NECESSARI:
DESCRIZIONE:

Prima di iniziare, pulisci il piano di lavoro e gli strumenti da disegno. Usando un foglio F4 liscio, effettua la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le consegne.

FIGURA DI RIFERIMENTO:

PROCEDURA OPERATIVA

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

STEP #01 – con la riga o la squadretta, tracciamo la retta orizzontale “r” a circa 5 centimetri dal bordo inferiore del foglio;

STEP #02 – sulla retta, individuiamo un segmento A-B di misura data, pari al lato del quadrato da costruire;

STEP #03 – puntiamo adesso il compasso in A e con apertura a piacere tracciamo una circonferenza che intersecherà la retta “r” nei punti 1 e 2;

STEP #04 – puntiamo il compasso in 1 e con apertura 1-2, tracciamo un arco dalla parte superiore della retta “r”;

STEP #05 – allo stesso modo puntiamo il compasso con la stessa apertura sul punto 2 e tracciamo un arco opposto a partire dal punto 1;

STEP #06 – i due archi si intersecheranno in un punto che chiameremo 3; con la riga uniamo i punti A e 3 e tracciamo la semiretta passante per entrambi;

STEP #07 – puntiamo il compasso in A e con apertura A-B tracciamo un arco che intersecherà la retta “s” in un punto C;

STEP #08 – sempre con la stessa apertura A-B pari al lato del quadrato, puntiamo il compasso in C e tracciamo un archetto dal lato di B;

STEP #09 – allo stesso modo spostiamo il compasso in B sempre con la stessa apertura pari al lato del quadrato e tracciamo un altro archetto che intersecherà il precedente in un punto D;

STEP #10 – rinforziamo adesso il segmento A-C;

STEP #11 – uniamo poi il punto B ed il punto D;

STEP #12 – infine, uniamo il punto C con il punto D;

Ricordo che le linee colorate di rosso sono quelle che vanno rinforzate nel disegno.

VIDEO

PERPENDICOLARE a un ESTREMO di un SEGMENTO

 Disegno
Ott 132012
 

PerpendicolareEstremo

DESCRIZIONE:

Strumenti da Disegno: foglio F4 liscio gr.220, matita HB/2, squadrette, riga e compasso.

Livello: classi seconde.

Difficoltà: bassa.

Descrizione: usando un foglio dall’album da disegno, effettuiamo la squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le esercitazioni della scheda sopra.

PROCEDURA OPERATIVA:

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

  1. tracciare una retta orizzontale “r” per tutta la lunghezza del foglio, avendo cura di tracciarla leggermente più in basso della metà foglio;
  2. tracciare sopra le retta “r” un segmento AB lungo 15 centimetri spostato verso destra rispetto al centro del foglio;
  3. puntare il compasso sul punto A e tracciare una circonferenza con raggio a piacere; questa incontrerà la retta R nei punti 1 e 2;
  4. puntare, adesso, il compasso sul punto 2 con apertura 1-2 tracciare l’arco di circonferenza come in figura;
  5. allo stesso modo puntare il compasso sul punto 1 e tracciare un’altra circonferenza uguale e opposta alla precedente; i due archi si incontreranno nel punto 3;
  6. a questo punto basterà unire il punto 3 con il punto A per trovare la perpendicolare all’estremo del segmento AB come ricercato.

SCARICA L’ARTICOLO:

PERPENDICOLARE al PUNTO MEDIO di un SEGMENTO

 Didattica, Disegno
Ott 022012
 
PERPENDICOLARE PUNTO MEDIO SEGMENTO
Dati SEGMENTO A-B lungo 10 cm o secondo indicazione del docente
CONSEGNE:
Consegna 1 Esegui la costruzione geometrica
Digit Esegui le consegne in digitale utilizzando il CAD
DIFFICOLTA’ e CLASSE:
Livello Classe
STRUMENTI NECESSARI:
DESCRIZIONE:

Prima di iniziare, pulisci il piano di lavoro e gli strumenti da disegno. Usando un foglio F4 liscio, effettua la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le consegne.

PROCEDURA OPERATIVA

posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:

STEP #01 – posizioniamo la nostra riga o squadretta con inclinazione a piacere sul foglio e tracciamo per essa una retta r;

STEP #02 – tracciamo sulla retta r un segmento di lunghezza data A-B;

STEP #03 – adesso, puntiamo il compasso in A con apertura A-B pari alla lunghezza del segmento dato e tracciamo un arco di circonferenza su entrambi i lati della retta r;

STEP #04 – allo stesso modo, puntiamo il compasso in B con la stessa apertura A-B pari alla lunghezza del segmento dato e tracciamo un altro arco nella direzione opposta. È importante che i due archi si intersechino reciprocamente nei punti 1 e 2;

STEP #05 – per completare l’esercizio uniamo i punti 1 e 2 con il righello o la squadretta e tracciamo per essa una linea. Quest’ultima è la perpendicolare al punto medio del segmento A-B, ossia quella retta che passa esattamente per il suo centro e forma con essa un angolo di 90°.

VIDEO

1 2 … 11 12 13 14