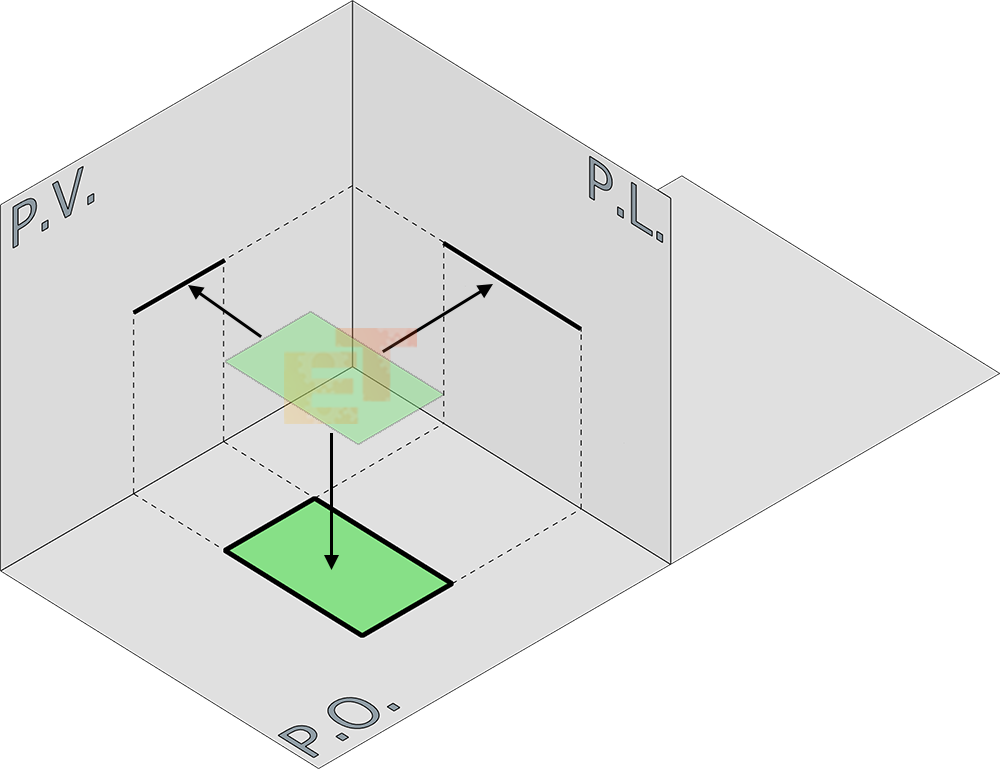
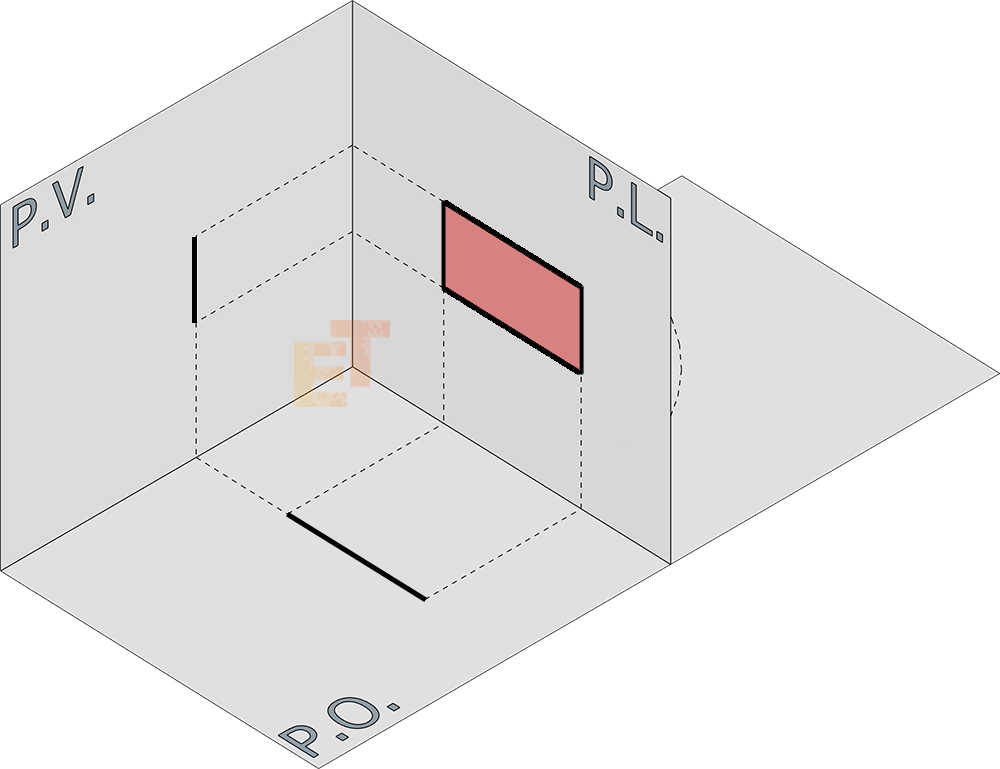
Abbiamo visto come con le Proiezioni Ortogonali, riusciamo a rappresentare un oggetto attraverso la sua scomposizione in tre proiezioni da altrettanti punti di vista e di come tale tecnica serva principalmente a descrivere metricamente un oggetto. Abbiamo poi visto come con le Assonometrie riusciamo a dare una rappresentazione tridimensionale rapida e intuitiva dell’oggetto e di come esistano differenti tipi di visualizzazione a seconda di come posizioniamo gli assi di riferimento.
Esiste un’altra tecnica grafica per la rappresentazione dei disegni geometrici che prende il nome di Prospettiva. La prospettiva, altro non è che un artificio geometrico che consente di rappresentare su una superficie piana un oggetto così come appare all’occhio umano. Quindi, tra le tecniche di rappresentazione è quella che consente una visualizzazione degli oggetti più vicina alla realtà.
 I primi esempi dell’uso della prospettiva compaiono nell’arte figurativa romana in modo embrionale, privo di regole e codifiche precise. Si parla più che altro di un tentativo di rappresentazione prospettica basata sulla sensibilità e sull’intuito dell’artista. Una vera e propria rivoluzione della tecnica la si ebbe nel quattordicesimo secolo ad opera dell’artista e architetto Filippo Brunelleschi (1377 – 1446). Con la sua grande maestria e la conoscenza approfondita del disegno tecnico, l’architetto fiorentino adotta per la prima volta il sistema di rappresentazione prospettica a un unico punto di fuga, per cui ne è anche l’inventore. La diffusione di questa tecnica fu rapida e accolta ben volentieri, perché in un’epoca di rinnovamento come il Rinascimento anche le novità nel disegno rappresentavano una svolta in quella direzione.
I primi esempi dell’uso della prospettiva compaiono nell’arte figurativa romana in modo embrionale, privo di regole e codifiche precise. Si parla più che altro di un tentativo di rappresentazione prospettica basata sulla sensibilità e sull’intuito dell’artista. Una vera e propria rivoluzione della tecnica la si ebbe nel quattordicesimo secolo ad opera dell’artista e architetto Filippo Brunelleschi (1377 – 1446). Con la sua grande maestria e la conoscenza approfondita del disegno tecnico, l’architetto fiorentino adotta per la prima volta il sistema di rappresentazione prospettica a un unico punto di fuga, per cui ne è anche l’inventore. La diffusione di questa tecnica fu rapida e accolta ben volentieri, perché in un’epoca di rinnovamento come il Rinascimento anche le novità nel disegno rappresentavano una svolta in quella direzione.
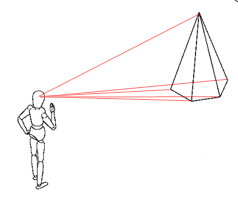 Brunelleschi basò il suo approccio sugli studi di Euclide della percezione visiva, ossia dei raggi luminosi che dall’oggetto si dirigono verso l’osservatore convergendo verso il centro dell’occhio sul piano della retina. Nella teoria formulata da Brunelleschi i raggi proiettanti sono rette che toccano i vertici degli oggetti che si devono rappresentare, il centro di proiezione è il punto di vista e la retina è il piano di rappresentazione.
Brunelleschi basò il suo approccio sugli studi di Euclide della percezione visiva, ossia dei raggi luminosi che dall’oggetto si dirigono verso l’osservatore convergendo verso il centro dell’occhio sul piano della retina. Nella teoria formulata da Brunelleschi i raggi proiettanti sono rette che toccano i vertici degli oggetti che si devono rappresentare, il centro di proiezione è il punto di vista e la retina è il piano di rappresentazione.
Il procedimento geometrico teorizzato da Brunelleschi fu completato e regolamentato da Piero della Francesca, verso la metà 1400. Egli scrisse il trattato “De prospectiva pingendi” che costituisce il primo studio organico della prospettiva con la formulazione di un preciso sistema di leggi e procedimenti matematici.
Dal rinascimento in poi la prospettiva sarà sempre più legata alle ricerca matematica, realizzando un passaggio dalla prospettiva rinascimentale di tipo centrale, a rappresentazioni su di un piano con modalità diverse (accidentale e obliqua). Questa parte della geometria prenderà il nome di Geometria Descrittiva.
 TORNA ALL’INDICE
TORNA ALL’INDICE
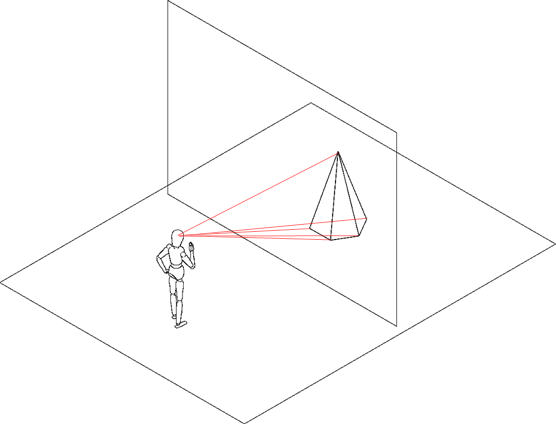 La prospettiva consente, quindi, di vedere gli oggetti esattamente come li percepisce l’occhio umano. Immaginiamo, quindi, di guardare un oggetto senza muovere la testa e contemporaneamente con tutti e due gli occhi (visione binoculare). Possiamo definire un cono visivo che partendo dall’occhio dell’osservatore includa tutto l’oggetto da osservare. Questo dipende ovviamente dalla dimensione dell’oggetto e dalla distanza dell’osservatore da questo. Dall’esperienza condotta scientificamente, si è dimostrato che l’angolo migliore di apertura del cono visivo deve essere compreso tra i 30° e i 40°. Coni ottici con apertura maggiore generano aberrazioni ottiche simili a quelle che i fotografi ottengono usando un grandangolare come obiettivo per la loro macchina fotografica.
La prospettiva consente, quindi, di vedere gli oggetti esattamente come li percepisce l’occhio umano. Immaginiamo, quindi, di guardare un oggetto senza muovere la testa e contemporaneamente con tutti e due gli occhi (visione binoculare). Possiamo definire un cono visivo che partendo dall’occhio dell’osservatore includa tutto l’oggetto da osservare. Questo dipende ovviamente dalla dimensione dell’oggetto e dalla distanza dell’osservatore da questo. Dall’esperienza condotta scientificamente, si è dimostrato che l’angolo migliore di apertura del cono visivo deve essere compreso tra i 30° e i 40°. Coni ottici con apertura maggiore generano aberrazioni ottiche simili a quelle che i fotografi ottengono usando un grandangolare come obiettivo per la loro macchina fotografica.
L’altro fattore fondamentale per una buona riuscita della prospettiva è la scelta del punto di vista. E’ facile intuire come sia possibile guardare un oggetto in infiniti modi e di come questo dipenda da tre parametri fondamentali: posizione dell’osservatore, distanza tra l’osservatore e l’oggetto e l’altezza del punto di vista. Ad esempio, nella prospettiva accidentale, l’asse visuale va collocato in corrispondenza della parte dell’oggetto che si vuole evidenziare (ad esempio un lato dell’oggetto piuttosto che un altro).
Per capire come ciò avviene, è necessario definire alcuni elementi base della tecnica prospettica. In pratica si tratta di osservare un oggetto e quindi di definire un osservatore (noi), scegliere l’oggetto da rappresentare, e immaginare di frapporre tra noi e l’oggetto un piano virtuale verticale, come una lastra di vetro trasparente, che rappresenta il piano sul quale disegneremo il nostro oggetto in prospettiva.
Vediamo quali sono gli elementi base della prospettiva:
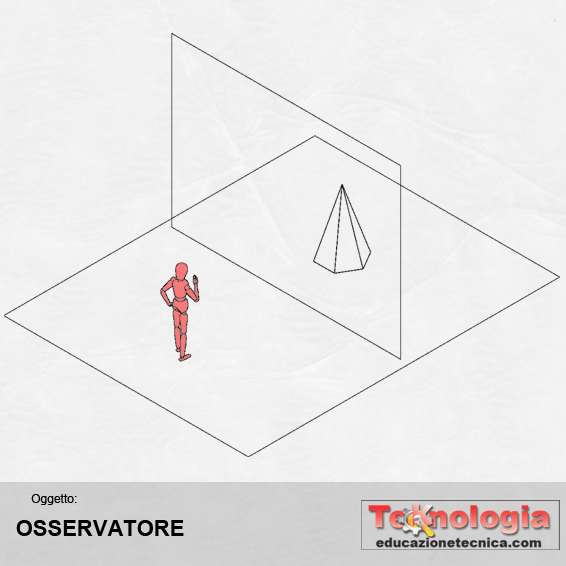 |
OSSERVATORE – siamo noi, cioè coloro che osservano l’oggetto da una posizione ben precisa |
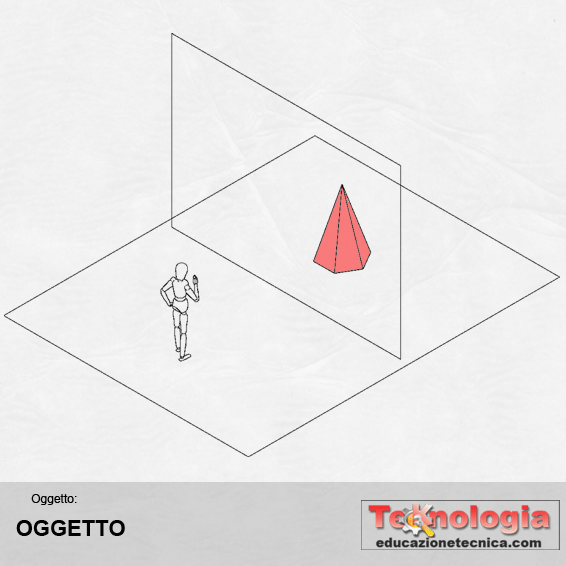 |
OGGETTO – qualunque cosa vogliamo rappresentare in prospettiva; viene definita anche figura obiettiva |
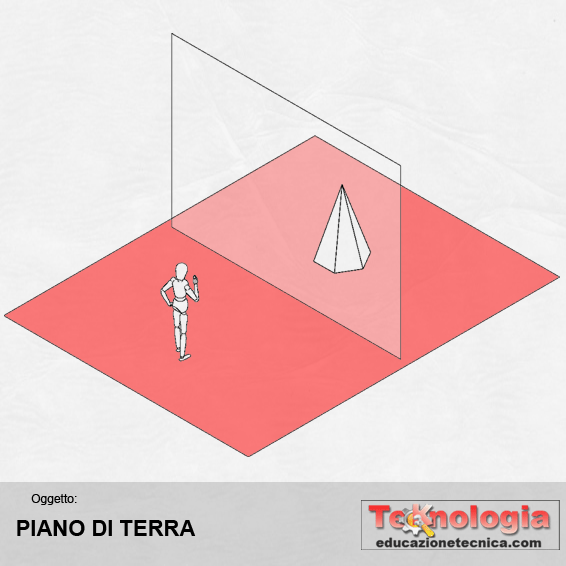 |
PIANO DI TERRA (PT) – è il piano orizzontale sul quale è collocato l’osservatore. Rappresenta in parole povere il pavimento sotto i nostri piedi. Si indica con le lettere P e T maiuscole |
 |
QUADRO PROSPETTICO (Q) – rappresenta il piano verticale interposto tra l’osservatore e la figura obiettiva; possiamo immaginarlo come una lastra di vetro posta verticalmente tra noi e l’oggetto che vogliamo rappresentare. Si indica con la lettera Q maiuscola |
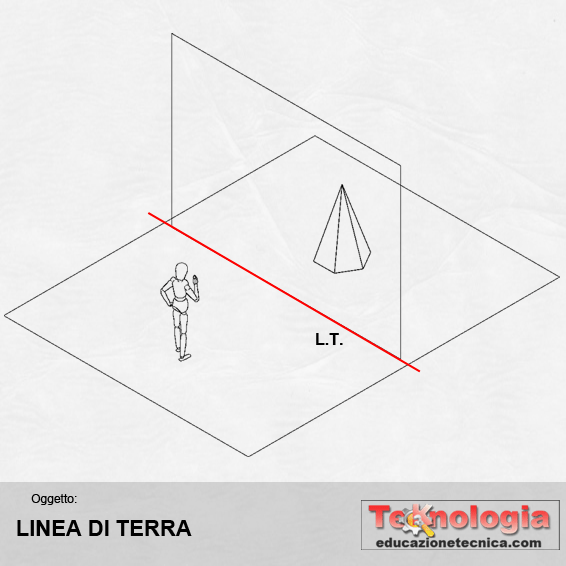 |
LINEA DI TERRA (LT) – rappresenta la linea di intersezione tra il piano di terra PT dove è poggiato l’osservatore e il piano di quadro prospettico Q. Si indica con le lettere L e T maiuscole |
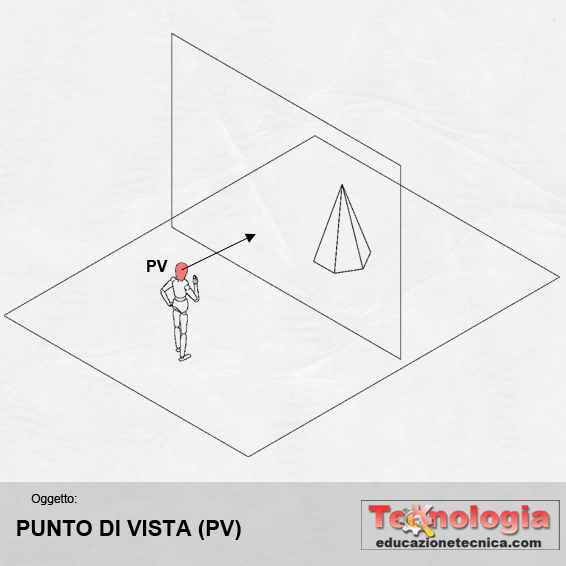 |
PUNTO DI VISTA (PV) – rappresenta il punto dal quale guardiamo l’oggetto; quindi sono i nostri occhi. Si indica con le lettere P e V maiuscole |
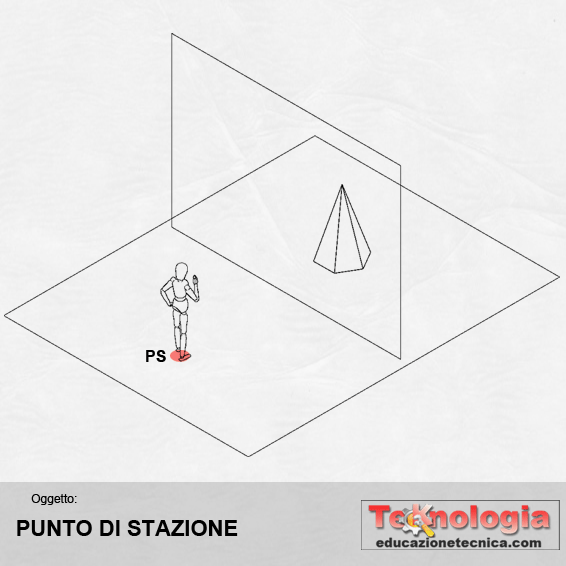 |
PUNTO DI STAZIONE (PS) – rappresenta il punto esatto sul piano di terra PT dove si trova l’osservatore. Quindi il punto nel quale poggiamo i nostri piedi. Si indica con le lettere P e S maiuscole |
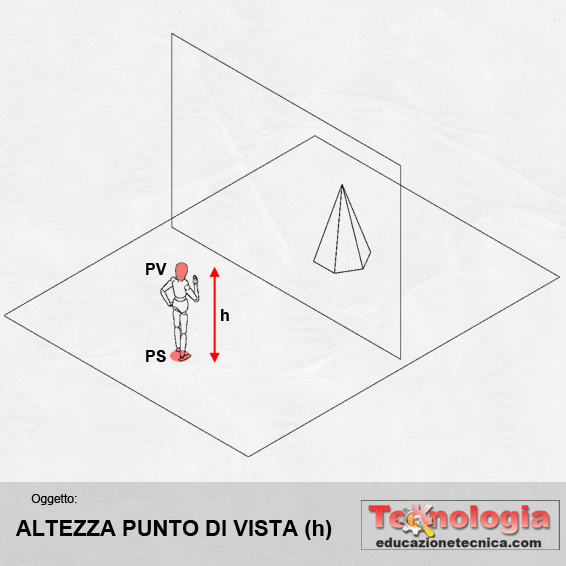 |
ALTEZZA (h) – rappresenta la distanza tra il punto di vista dell’osservatore PV e il punto di stazione PS dell’osservatore stesso. Si indica con la lettera h minuscola |
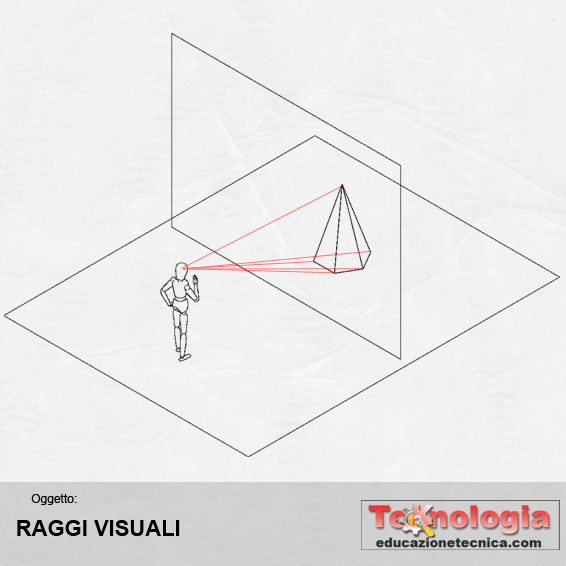 |
RAGGI VISUALI – rappresentano tutte le rette virtuali che collegano il punto di vista, ossia l’occhio dell’osservatore, con tutti gli spigoli dell’oggetto da rappresentare |
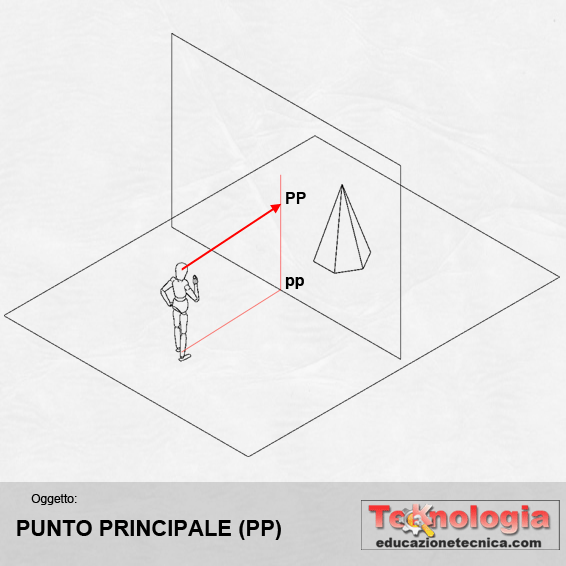 |
PUNTO PRINCIPALE (PP) – rappresenta il punto in cui l’asse visivo ortogonale che parte dall’occhio dell’osservatore, incontra il quadro prospettico Q. Si indica con le lettere PP maiuscole |
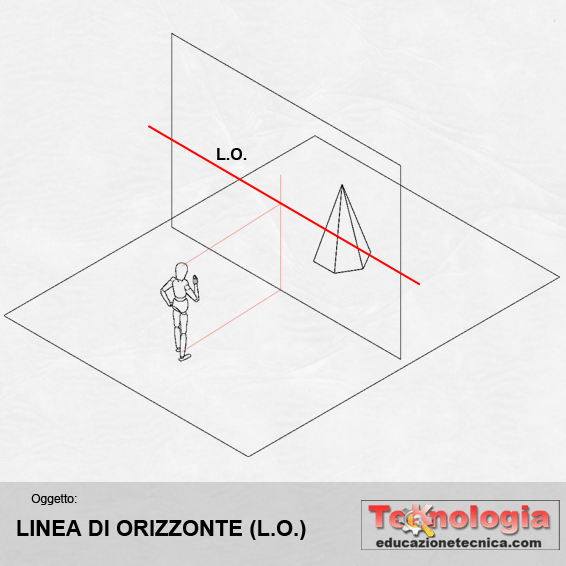 |
LINEA DI ORIZZONTE (LO) – rappresenta la linea di intersezione tra il piano orizzontale parallelo al piano di terra passante per l’occhio dell’osservatore (PV). e il quadro prospettico Q. La linea di orizzonte varia al variare dell’altezza dell’osservatore. Si indica con le lettere L e O maiuscole |
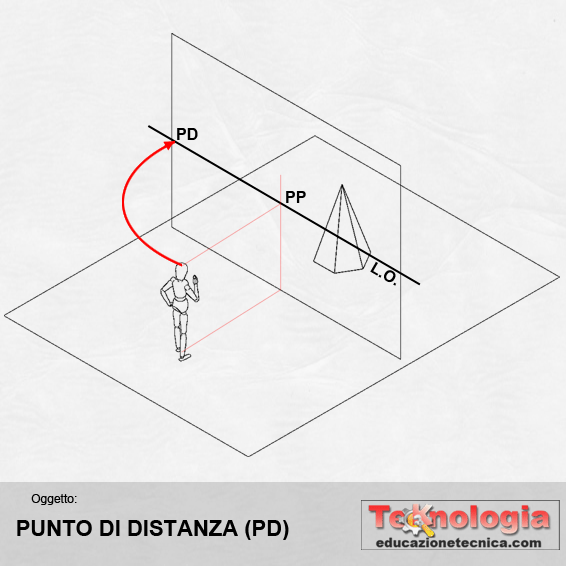 |
PUNTO DI DISTANZA (PD) – rappresenta la distanza del punto di vista PV dal piano di quadro Q. Serve a facilitare le rappresentazioni grafiche e si riporta a destra o a sinistra del Punto Principale PP sulla Linea di Orizzonte LO. Si indica con le lettere P e D maiuscole |
 TORNA ALL’INDICE
TORNA ALL’INDICE
In molti casi, la realizzazione di una prospettiva corretta, richiede la preparazione di un disegno che rappresenti in vista dall’alto (pianta) l’oggetto da rappresentare e sul quale siano note e indicate le dimensioni dell’oggetto stesso. Questo disegno prende il nome di figura preparatoria. La realizzazione di questa figura, su foglio a parte o su un angolo dello stesso foglio, permette di realizzare una prospettiva in modo più semplice e diretto, e in molti casi anche in scala diversa generalmente più grande. Per cui, la figura preparatoria, rappresenta in molti casi un grande vantaggio nella realizzazione della prospettiva.
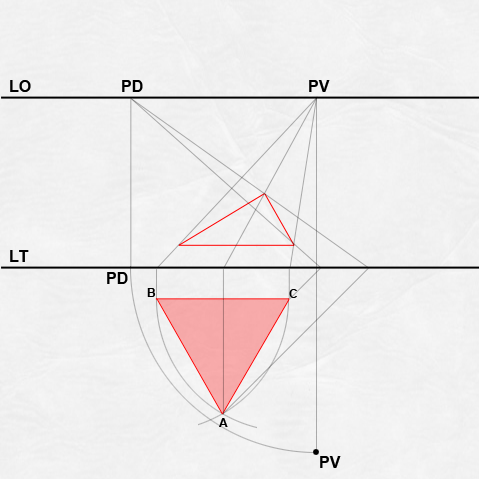
Prospettiva con figura preparatoria di un Triangolo Equilatero
Sulla base delle teorizzazioni sviluppate da allora, possiamo dire che esistono tre tipi di rappresentazione prospettica che variano in base alla posizione che l’oggetto assume rispetto a un piano di proiezione detto quadro. Per cui avremo:
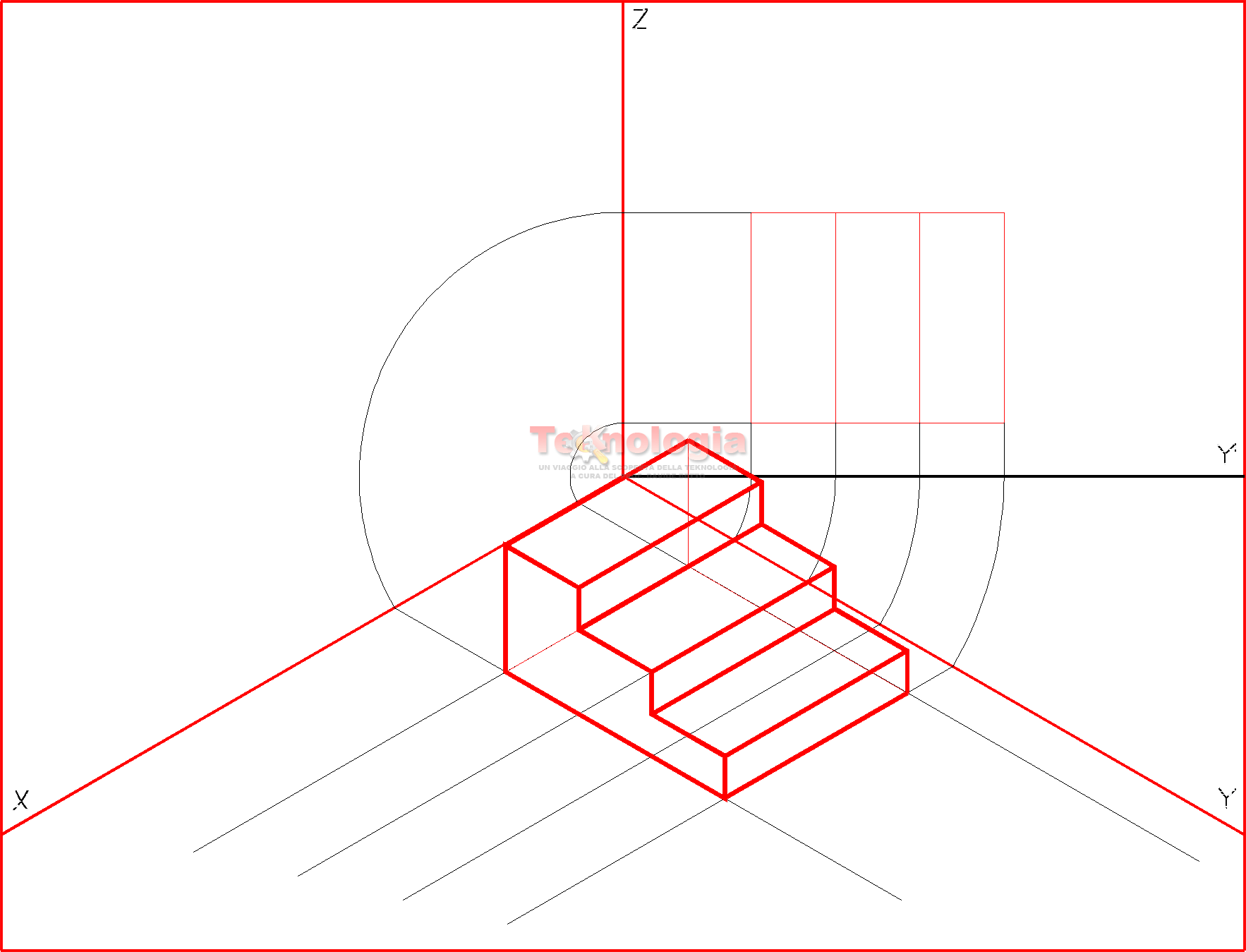
- prospettiva centrale o frontale; l’oggetto da disegnare è parallelo al piano di proiezione. Tutte le linee di profondità (lunghezza) convergono nello stesso punto (punto di fuga proprio), le linee parallele al quadro (larghezza) restano parallele, le rette verticali (altezza) restano verticali;
- prospettiva accidentale o d’angolo; l’oggetto rappresentato è ruotato rispetto al quadro e nessuno dei suoi lati è a questo parallelo, vi sono così due punti di fuga in cui convergo le linee orizzontali (larghezza e lunghezza), ma le rette verticali (altezza) restano verticali;
- prospettiva obliqua o razionale o a quadro inclinato; l’oggetto rappresentato è ruotato rispetto al quadro di proiezione anche verticalmente, vi sono così tre punti di fuga, due per le linee orizzontali (larghezza e lunghezza) ed uno per quelle verticali (altezza).
 TORNA ALL’INDICE
TORNA ALL’INDICE
PROSPETTIVA CENTRALE O FRONTALE
|
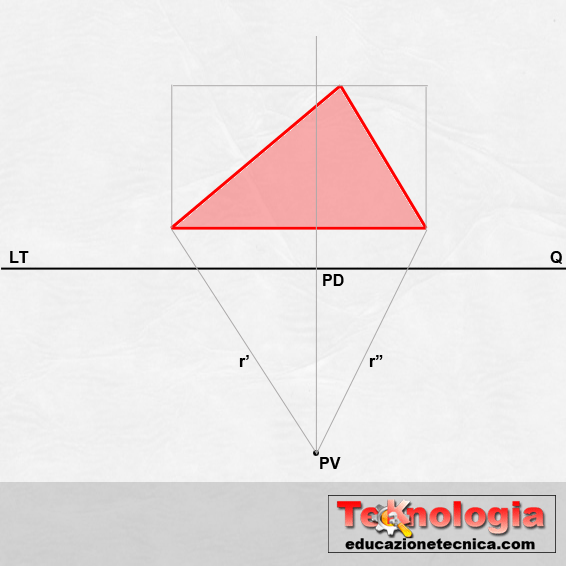 Come detto precedentemente, nella prospettiva centrale, la posizione del piano di quadro Q è sempre parallela a un lato della figura o a un lato del quadrato o rettangolo che la contiene. Le rette parallele al quadro restano parallele anche in prospettiva e le rette verticali restano tali anche in prospettiva.
Come detto precedentemente, nella prospettiva centrale, la posizione del piano di quadro Q è sempre parallela a un lato della figura o a un lato del quadrato o rettangolo che la contiene. Le rette parallele al quadro restano parallele anche in prospettiva e le rette verticali restano tali anche in prospettiva.
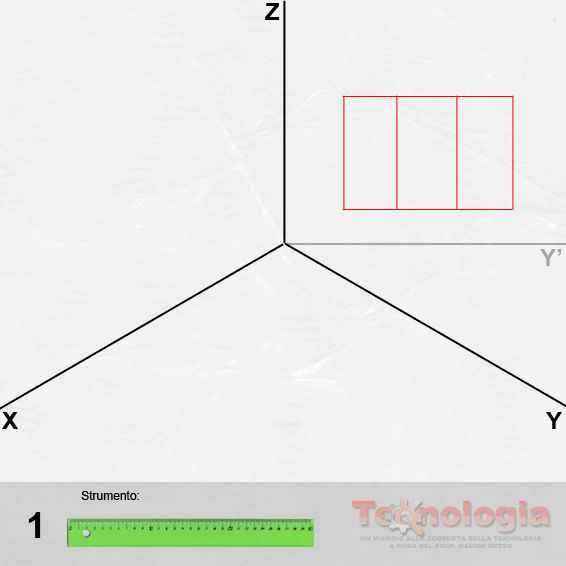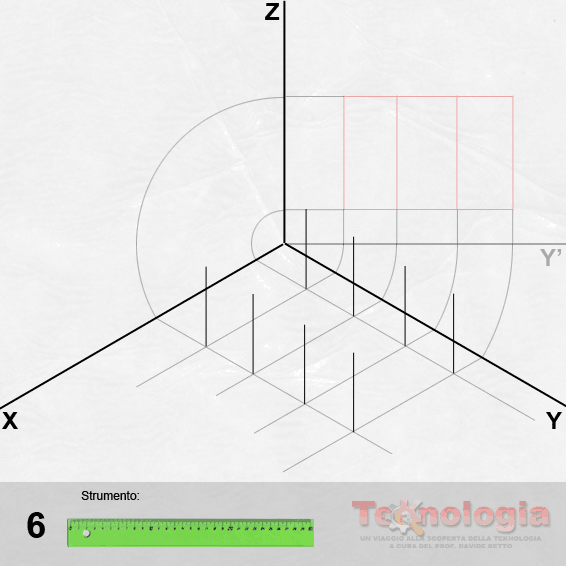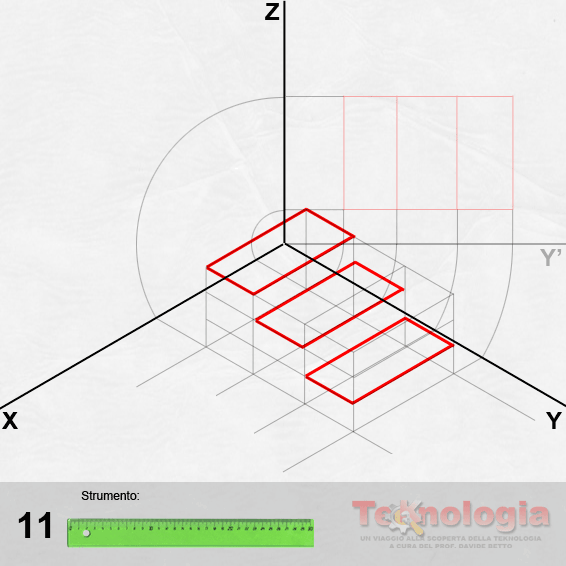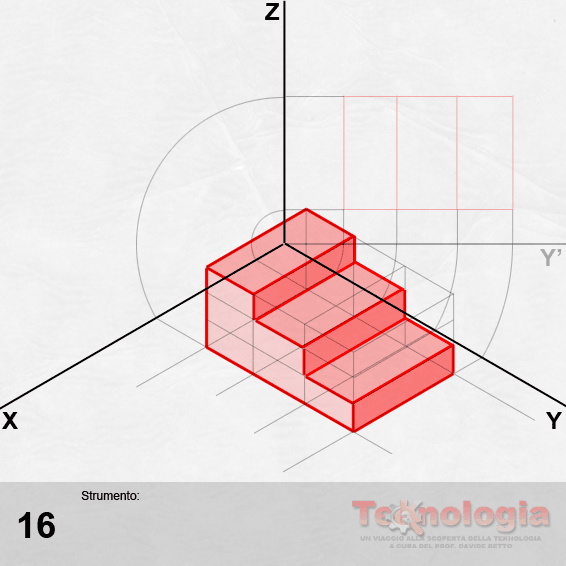
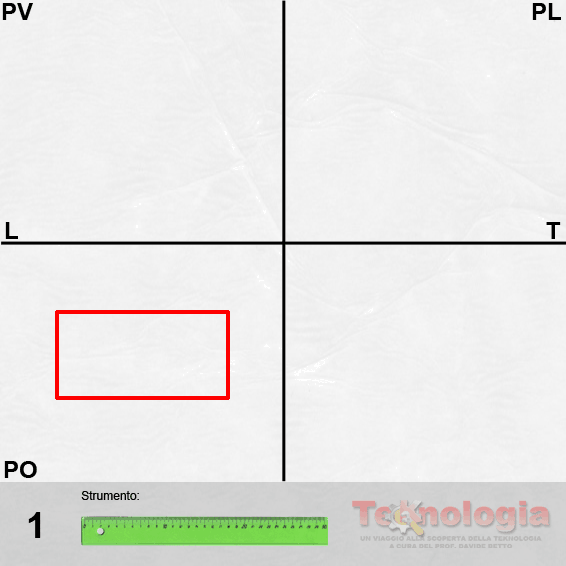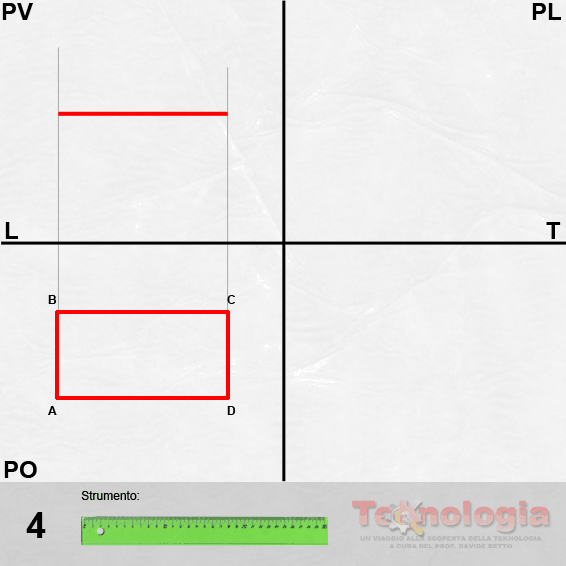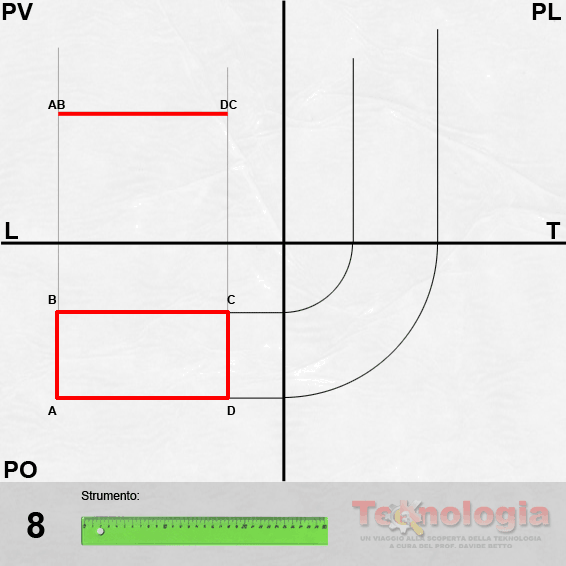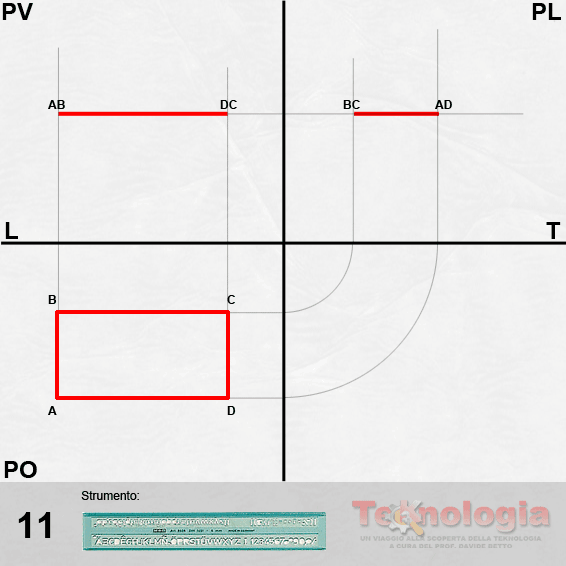
L’operazione preliminare per la prospettiva centrale, è la definizione in proiezione ortogonale delle dimensioni della figura. Bisogna quindi disegnare una figura preparatoria che prevede i seguenti passaggi:
disegnare la pianta della figura da rappresentare in prospettiva della quale, ovviamente, bisogna conoscere le dimensioni corrette;
costruire il piano di quadro (Q) in posizione parallela ad uno dei lati della figura;
si posiziona il punto di vista (PV) a una distanza tale che la figura rientri completamente nel cono visivo (normalmente una visuale con angolo di apertura non superiore ai 35° e in una posizione tale che l’asse visivo passi all’interno della figura, nel suo centro o vicino a questo;
si ribalta il punto di vista PV sulla linea di orizzonte LO individuando il punto di distanza PD;
si ribaltano i punti utili alla definizione della prospettiva sul lato opposto a PD tracciando delle rette inclinate a 45°.
Nella prospettiva centrale si possono utilizzare diversi metodi per ottenere l’immagine desiderata. Quelli più utilizzati sono:
Il metodo dei raggi visuali;
Il metodo del prolungamento dei lati;
Il metodo dei punti di distanza;
Il sistema del ribaltamento.
 TORNA ALL’INDICE
TORNA ALL’INDICE
PROSPETTIVA ACCIDENTALE O D’ANGOLO
|
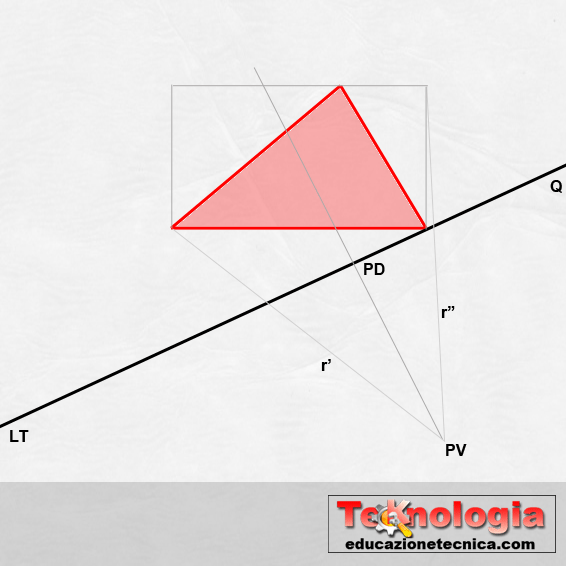 Nella prospettiva accidentale,come detto, il piano di quadro Q non è parallelo ai lati dell’oggetto da rappresentare. La disposizione del piano dipende dall’effetto prospettico che si vuole ottenere. Una buona prospettiva si ottiene disponendo il quadro, nella figura preparatoria, con inclinazioni di 30° o 60° rispetto ai lati del rettangolo che contiene l’oggetto. E’ importante che l’angolo minore stia dal lato più importante della costruzione, cioè quello che vogliamo mettere in evidenza nella rappresentazione.
Nella prospettiva accidentale,come detto, il piano di quadro Q non è parallelo ai lati dell’oggetto da rappresentare. La disposizione del piano dipende dall’effetto prospettico che si vuole ottenere. Una buona prospettiva si ottiene disponendo il quadro, nella figura preparatoria, con inclinazioni di 30° o 60° rispetto ai lati del rettangolo che contiene l’oggetto. E’ importante che l’angolo minore stia dal lato più importante della costruzione, cioè quello che vogliamo mettere in evidenza nella rappresentazione.
La scelta del punto di vista è importantissima per una buona riuscita del disegno. Anche in questo caso la sua posizione è arbitraria ma è consigliabile posizionare PV a una distanza tale che l’angolo formato tra i raggi visuali r’ ed r” (i raggi che da PV vengono diretti verso gli estremi della figura rappresentata in pianta), sia minore di 45°. In questo modo, i raggi visuali staranno all’interno del cono ottico e quindi l’immagine risultante sarà percettivamente corretta, quindi senza aberrazioni ottiche.
Nella prospettiva accidentale si possono utilizzare diversi metodi per ottenere l’immagine desiderata. Quelli più utilizzati sono:
Il metodo dei raggi visuali;
Il metodo dei punti di distanza;
Il metodo dei punti di fuga e delle perpendicolari al quadro;
Il metodo dei punti misuratori.
 TORNA ALL’INDICE
TORNA ALL’INDICE
In questo caso, pure il Piano di Quadro Q è inclinato rispetto all’oggetto per cui anche le facce verticali dell’oggetto avranno un punto di fuga. Possiamo scegliere se il Piano di Quadro debba essere inclinato verso l’oggetto o verso l’osservatore.
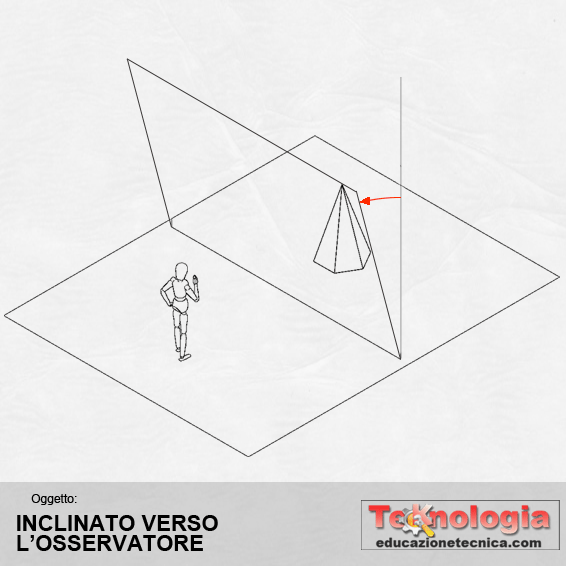
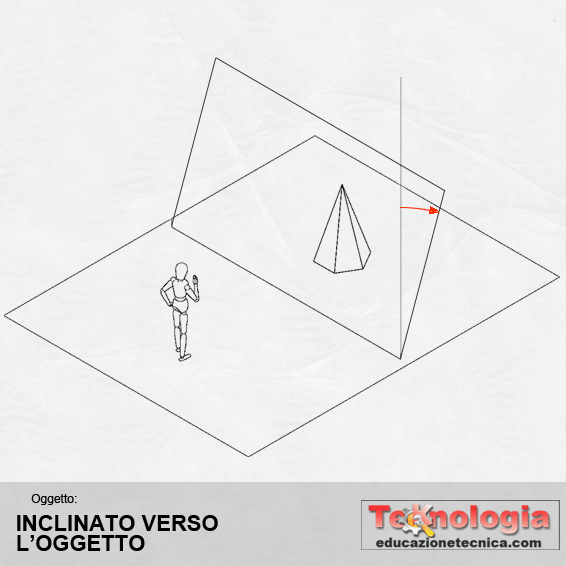
La prospettiva che si ottiene si chiamerà di conseguenza, prospettiva razionale dall’alto o prospettiva razionale dal basso. Questa prospettiva presenta maggiori difficoltà esecutive in confronto ai casi precedenti, per cui è raramente utilizzata. Inoltre il quadro può essere esterno, tangente o secante l’oggetto da rappresentare. Nel caso in cui sia secante, il quadro funge anche da Piano di Sezione come avviene negli spaccati prospettici.
Altro parametro da modificare che ci consente di ottenere differenti visualizzazioni dell’oggetto, è la quota del punto di vista PD rispetto all’oggetto da rappresentare. Quindi, potremo avere differenti visualizzazioni:
dal sotto in su, quando il punto di vista ha quota negativa, ossia quando viene posto più in basso della Linea di terra LT;
dal basso, quando il punto di vista è molto vicino alla Linea di terra LT fino a giacere su di essa. Avremo una prospettiva a raso terra, nella quale di conseguenza la linea di orizzonte coincide con la linea di terra;
ad altezza uomo, quando il punto di vista viene disposto a una quota variabile fra i 150 e 170 centimetri da terra. Questa rappresentazione ci consente di vedere gli oggetti come ci appaiono normalmente;
dall’alto, quando il punto di vista è situato a un’altezza maggiore di quella degli oggetti da rappresentare, così come avviene nelle viste dette a volo d’uccello.
 TORNA ALL’INDICE
TORNA ALL’INDICE
Creare o dividere segmenti in parti uguali in prospettiva, soprattutto in quella centrale può essere lungo e tedioso. Però, si può utilizzare uno stratagemma, chiamato metodo della X, per creare segmenti equidistanti o dividere segmenti in parti uguali. Vediamo come fare.
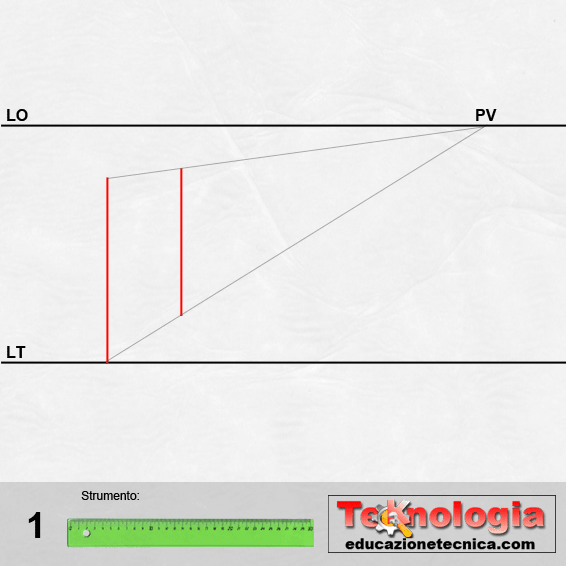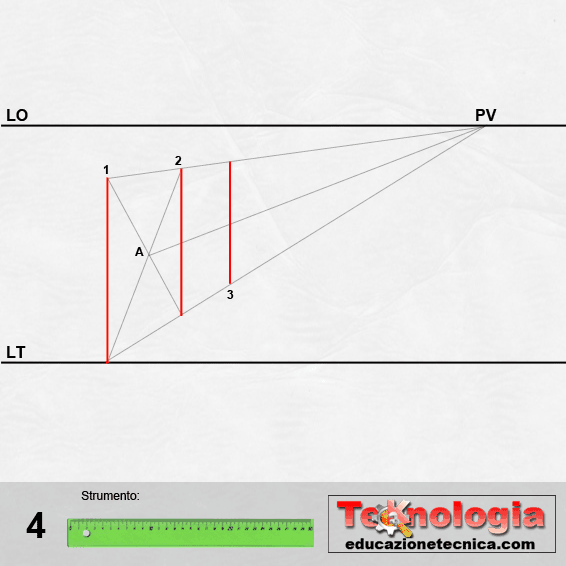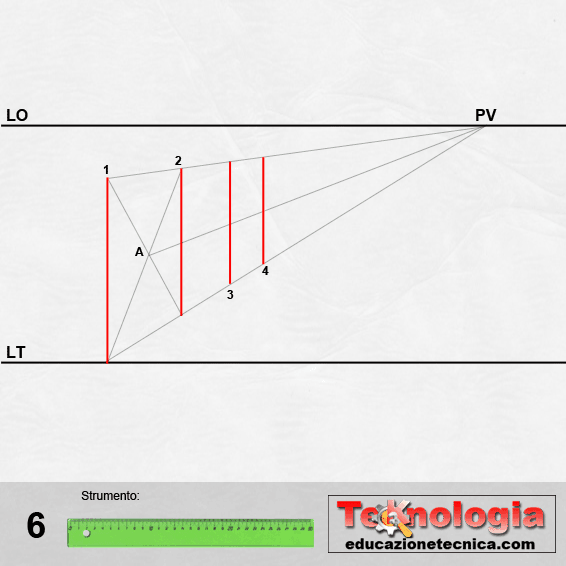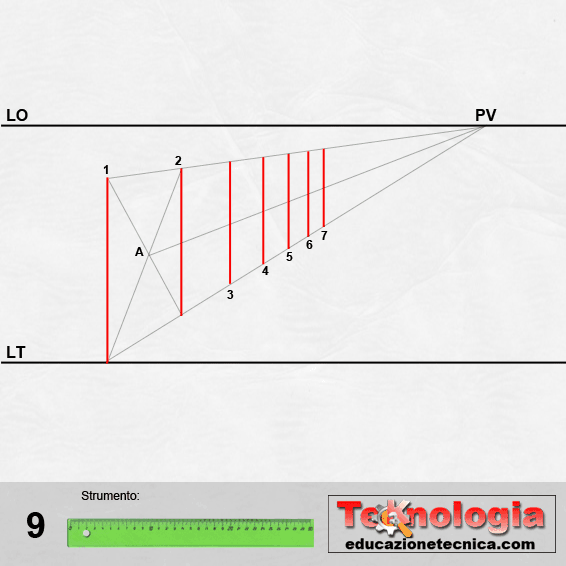
Immaginiamo di aver già fissato la LT e la LO e di aver individuato su LO il punto di fuga PV.
Tracciamo da un punto su LT una retta 1 e fughiamo su PV il suo punto base e la sua altezza.
Ad una certa distanza tracciamo un’altra retta verticale parallela a 1 che chiameremo retta 2.
Tracciamo adesso le diagonali tra i punti base delle due rette e le loro altezze; si disegnerà così una X (ecco da dove il nome di metodo della X).
Chiamiamo A il punto di intersezione tra le due diagonali e fughiamolo su PV.
Ora uniamo l’altezza della retta 1 con il punto medio sulla retta 2.
Dall’intersezione di questa retta con la fuga del punto di base della retta 1 individueremo il punto 3, base della retta 3 parallela alle due precedenti.
Allo stesso modo, dall’altezza della retta 2, tracciamo un segmento che interseca la retta 3 nel suo punto medio fino all’intersezione con la fuga del punto base della retta 1 che, individuerà un punto 4.
Da questo punto tracceremo la retta 4 parallela alle precedenti.
Procedendo analogamente, definiremo una serie di linee parallele, equidistanti, rappresentate in proiezione prospettica (vedi l’animazione sopra).
 TORNA ALL’INDICE
TORNA ALL’INDICE
IL METODO DEI PUNTI DI DISTANZA
|
Dobbiamo ad un altro grande architetto del passato, Leon Battista Alberti, la costruzione abbreviata in prospettiva che usa i cosiddetti punti di distanza, ossia rette inclinate a 45° rispetto al piano di quadro (Q) ottenute ribaltando sulla linea di orizzonte LO, la distanza del punto di vista PV dal quadro. L’uso dei punti di distanza, facilita moltissimo la costruzione delle figure in prospettiva centrale. Infatti, ogni punto può essere individuato dall’intersezione di una linea passante per il punto perpendicolare al quadro (che in prospettiva concorre al punto principale PP) con una linea, passante per il punto, inclinata di 45° rispetto al quadro (che in prospettiva concorre a un punto di distanza PD). In genere è sufficiente l’uso di un solo punto di distanza.

 TORNA ALL’INDICE
TORNA ALL’INDICE
MAPPA CONCETTUALE DELL’ARGOMENTO
|
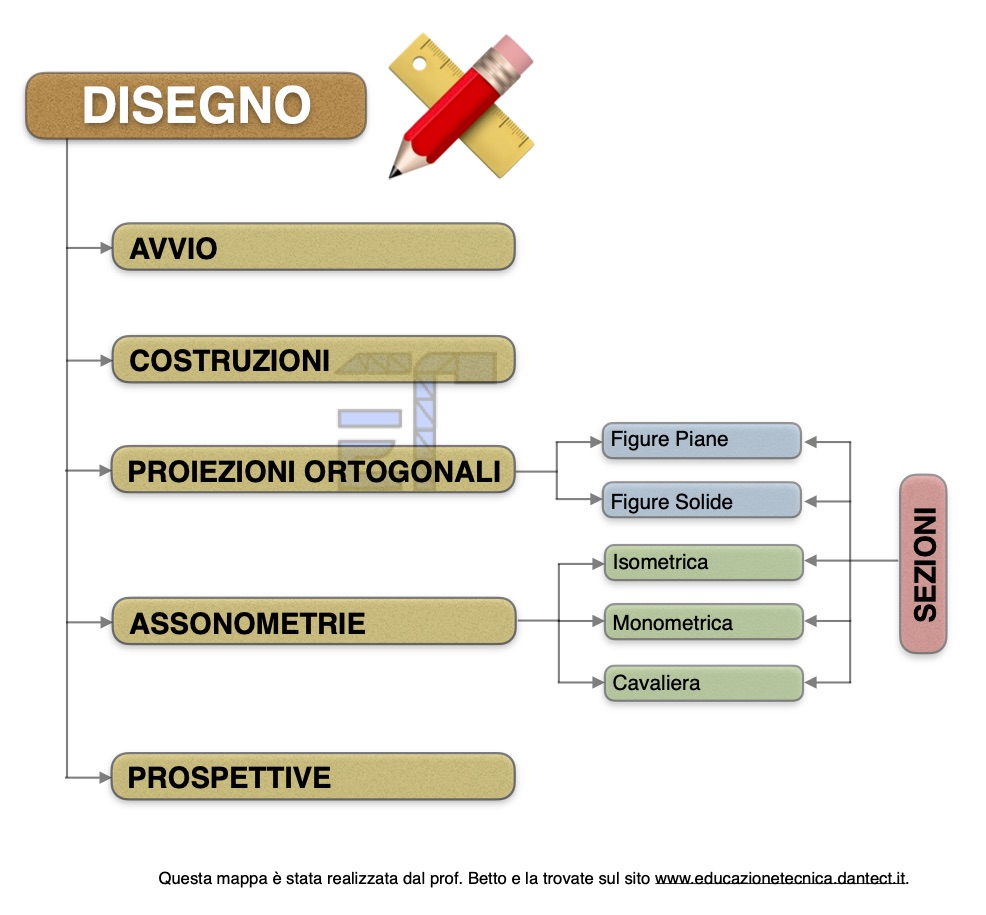
 TORNA ALL’INDICE
TORNA ALL’INDICE



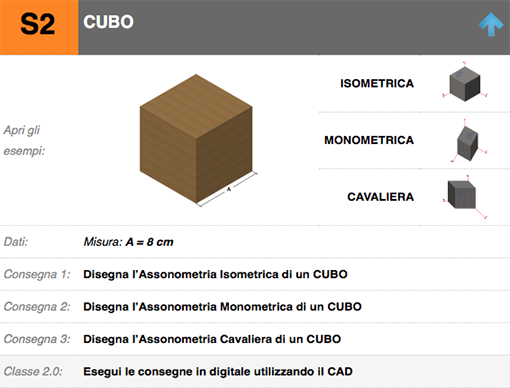
 Qui comodi sotto-menu consentono di navigare tra le sezioni del Disegno Tecnico e le altre aree specifiche per questo settore.
Qui comodi sotto-menu consentono di navigare tra le sezioni del Disegno Tecnico e le altre aree specifiche per questo settore.





 La prima codifica la si ebbe ad opera dell’architetto fiorentino
La prima codifica la si ebbe ad opera dell’architetto fiorentino 
 Immaginiamo di guardare una scena senza muovere la testa contemporaneamente con tutti e due gli occhi (visione binoculare). Tutto ciò che viene inquadrato all’interno dello spazio visibile dall’occhio, prende il nome di
Immaginiamo di guardare una scena senza muovere la testa contemporaneamente con tutti e due gli occhi (visione binoculare). Tutto ciò che viene inquadrato all’interno dello spazio visibile dall’occhio, prende il nome di 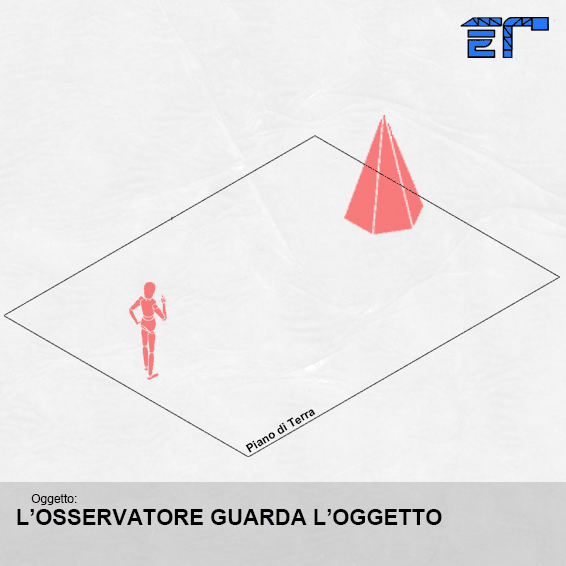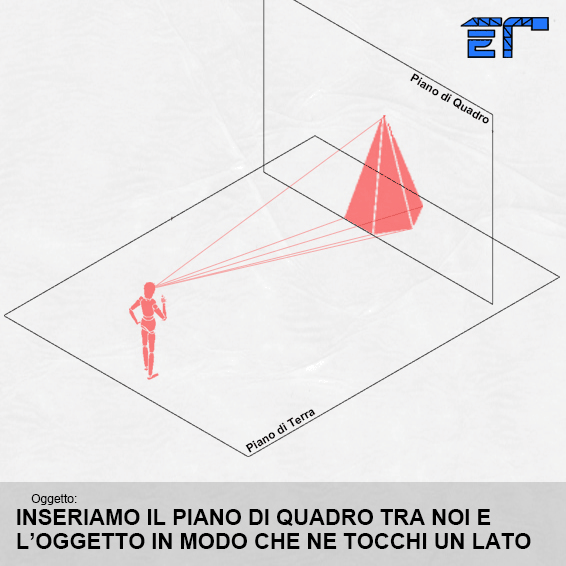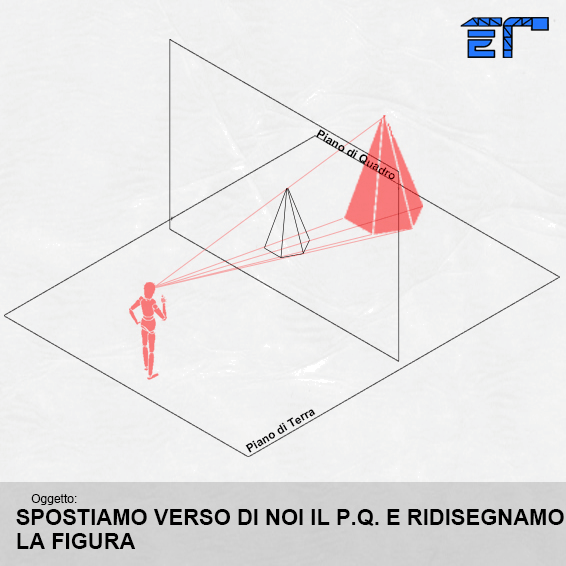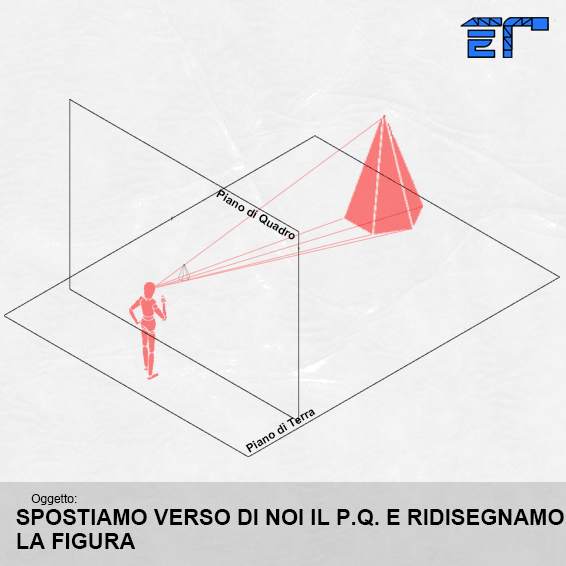













 Iniziamo ad approfondire la nostra conoscenza sugli strumenti della palette DISEGNO e ovviamente iniziamo con i comandi LINEA e POLILINEA. Tracciare linee in un C.A.D., è una cosa relativamente semplice, ma saperne tracciare una correttamente, di una determinata lunghezza o in una specifica direzione non lo è altrettanto. Però, basta soltanto entrare nella logica di questi programmi per rendersi conto di come possa risultare intuitivo e immediato farlo.
Iniziamo ad approfondire la nostra conoscenza sugli strumenti della palette DISEGNO e ovviamente iniziamo con i comandi LINEA e POLILINEA. Tracciare linee in un C.A.D., è una cosa relativamente semplice, ma saperne tracciare una correttamente, di una determinata lunghezza o in una specifica direzione non lo è altrettanto. Però, basta soltanto entrare nella logica di questi programmi per rendersi conto di come possa risultare intuitivo e immediato farlo.
 Selezionare un comando in un C.A.D. è possibile in diversi modi. Possiamo, ad esempio, selezionare il comando LINEA direttamente dalla palette DISEGNO oppure selezionando la voce LINEA dal menu DISEGNO o semplicemente digitando sulla tastiera la lettera L (abbreviazione di LINEA) e il tasto INVIO.
Selezionare un comando in un C.A.D. è possibile in diversi modi. Possiamo, ad esempio, selezionare il comando LINEA direttamente dalla palette DISEGNO oppure selezionando la voce LINEA dal menu DISEGNO o semplicemente digitando sulla tastiera la lettera L (abbreviazione di LINEA) e il tasto INVIO. Il secondo punto dovrà essere spostato rispetto al primo di 7 centimetri lungo l’asse X e zero lungo Y.
Il secondo punto dovrà essere spostato rispetto al primo di 7 centimetri lungo l’asse X e zero lungo Y. 




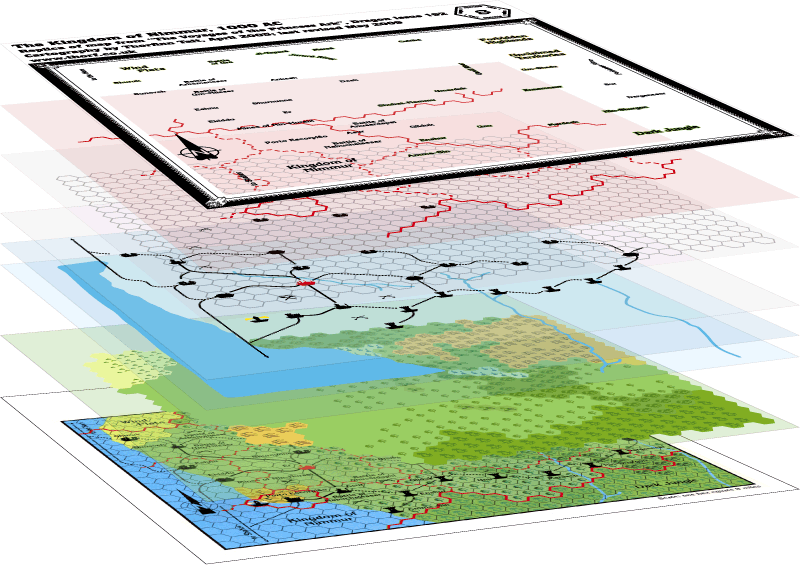 I C.A.D., lavorano per livelli, ossia come per i cartoni animati, possiamo posizionare oggetti diversi su più fogli trasparenti, costruendo il movimento dei personaggi semplicemente spostando uno o l’altro di questi fogli (l’immagine qui a lato, ci mostra come una planimetria possa essere ottenuta come sovrapposizione di elementi diversi: territorio, mare, strade, curve di livello, ecc.). L’immagine visualizzata sarà l’immagine complessiva della planimetria con tutti gli elementri insieme; il limite consiste nel fatto che potremo disegnare solo su di un LIVELLO, quello posto in primo piano. Ciò significa che se io voglio modificare ad esempio la mappa delle strade, dovrò posizionare in primo piano il livello con le “STRADE”. Ma vediamo praticamente come procedere.
I C.A.D., lavorano per livelli, ossia come per i cartoni animati, possiamo posizionare oggetti diversi su più fogli trasparenti, costruendo il movimento dei personaggi semplicemente spostando uno o l’altro di questi fogli (l’immagine qui a lato, ci mostra come una planimetria possa essere ottenuta come sovrapposizione di elementi diversi: territorio, mare, strade, curve di livello, ecc.). L’immagine visualizzata sarà l’immagine complessiva della planimetria con tutti gli elementri insieme; il limite consiste nel fatto che potremo disegnare solo su di un LIVELLO, quello posto in primo piano. Ciò significa che se io voglio modificare ad esempio la mappa delle strade, dovrò posizionare in primo piano il livello con le “STRADE”. Ma vediamo praticamente come procedere.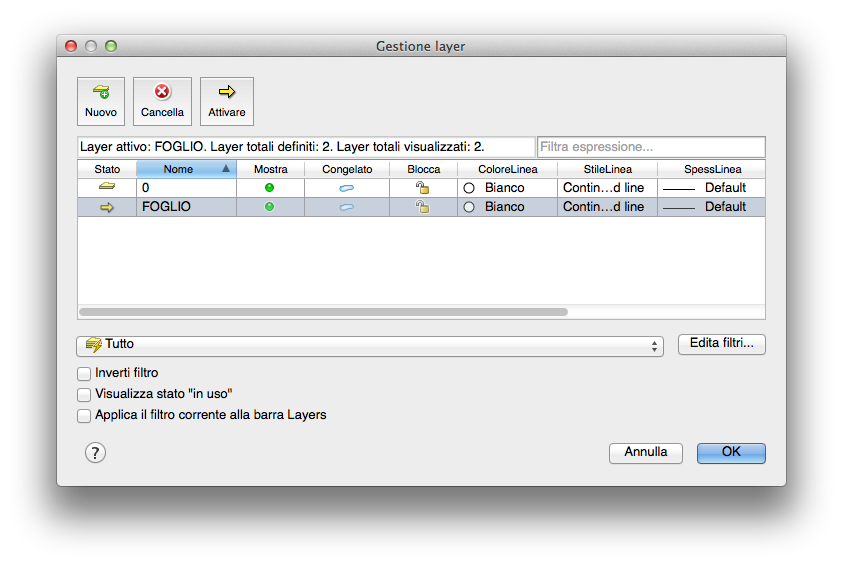

 Una sola precisazione, prima di iniziare: un programma C.A.D. realizza le immagini sullo schermo del computer attraverso una grafica di tipo vettoriale. La differenza è sostanziale rispetto al raster usato dai programmi di grafica classica come Photoshop o altri (per capirci la grafica delle fotografie). Infatti, una grafica raster disegna un’immagine sullo schermo assegnando a ciascun punto (pixel) una posizione assoluta tramite coordinate XY, colore e intensità. In questo modo si riesce a disegnare con precisione assoluta qualsiasi immagine. Il problema sorge quando la ingrandiamo. Essendo disegnata per punti, il computer li ingrandirà e conseguentemente l’immagine risulterà sgranata e poco definita (immagine c). Al contrario, la grafica vettoriale è definita attraverso equazioni matematiche, per cui l’immagine viene ricalcolata ogni volta e ogni dettaglio ricostruito con assoluta precisione (immagine b).
Una sola precisazione, prima di iniziare: un programma C.A.D. realizza le immagini sullo schermo del computer attraverso una grafica di tipo vettoriale. La differenza è sostanziale rispetto al raster usato dai programmi di grafica classica come Photoshop o altri (per capirci la grafica delle fotografie). Infatti, una grafica raster disegna un’immagine sullo schermo assegnando a ciascun punto (pixel) una posizione assoluta tramite coordinate XY, colore e intensità. In questo modo si riesce a disegnare con precisione assoluta qualsiasi immagine. Il problema sorge quando la ingrandiamo. Essendo disegnata per punti, il computer li ingrandirà e conseguentemente l’immagine risulterà sgranata e poco definita (immagine c). Al contrario, la grafica vettoriale è definita attraverso equazioni matematiche, per cui l’immagine viene ricalcolata ogni volta e ogni dettaglio ricostruito con assoluta precisione (immagine b). Iniziamo a lavorare con DraftSight e ci accorgiamo subito come questo abbia un’interfaccia pulita ma non proprio di immediata comprensione.
Iniziamo a lavorare con DraftSight e ci accorgiamo subito come questo abbia un’interfaccia pulita ma non proprio di immediata comprensione.


















 Brunelleschi basò il suo approccio sugli studi di Euclide della percezione visiva, ossia dei raggi luminosi che dall’oggetto si dirigono verso l’osservatore convergendo verso il centro dell’occhio sul piano della retina. Nella teoria formulata da Brunelleschi i raggi proiettanti sono rette che toccano i vertici degli oggetti che si devono rappresentare, il centro di proiezione è il punto di vista e la retina è il piano di rappresentazione.
Brunelleschi basò il suo approccio sugli studi di Euclide della percezione visiva, ossia dei raggi luminosi che dall’oggetto si dirigono verso l’osservatore convergendo verso il centro dell’occhio sul piano della retina. Nella teoria formulata da Brunelleschi i raggi proiettanti sono rette che toccano i vertici degli oggetti che si devono rappresentare, il centro di proiezione è il punto di vista e la retina è il piano di rappresentazione.