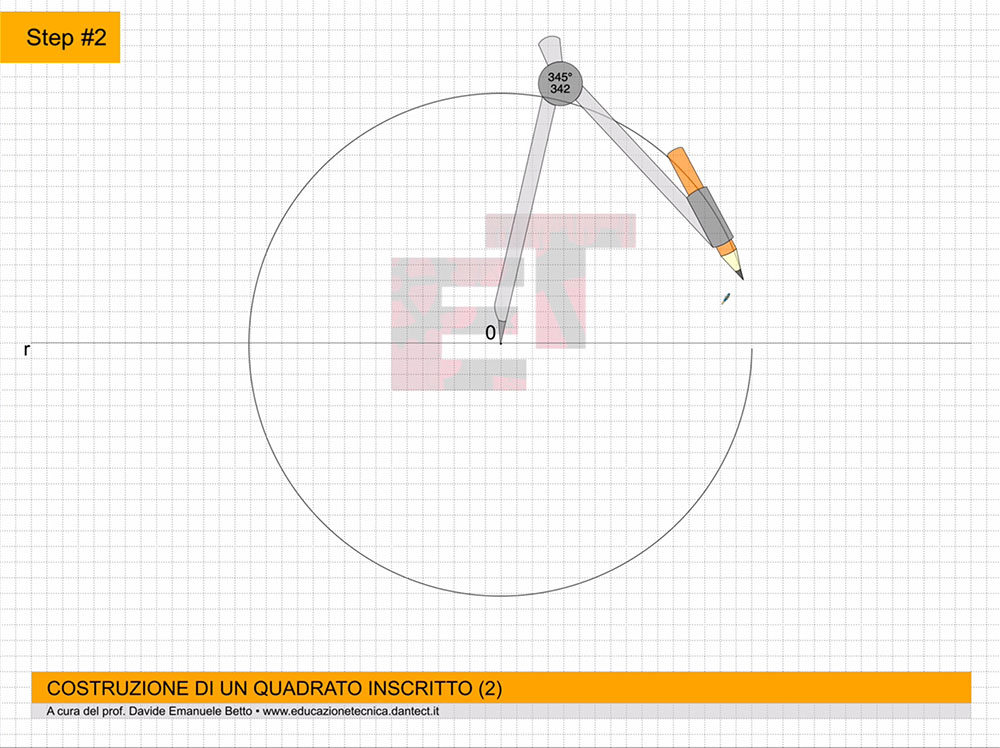
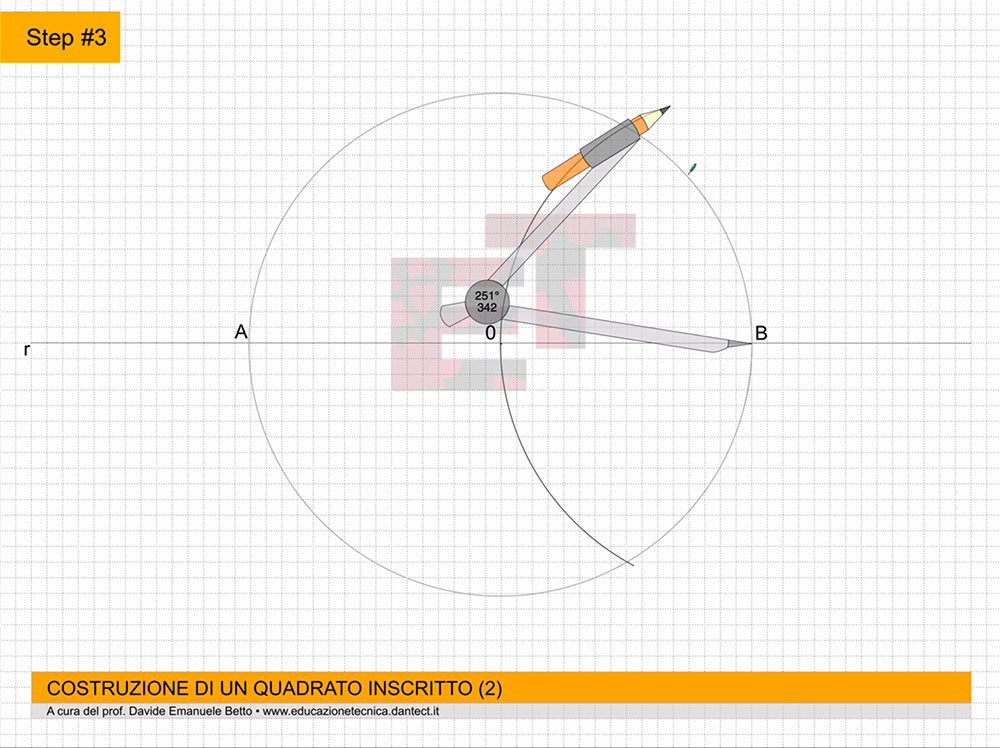
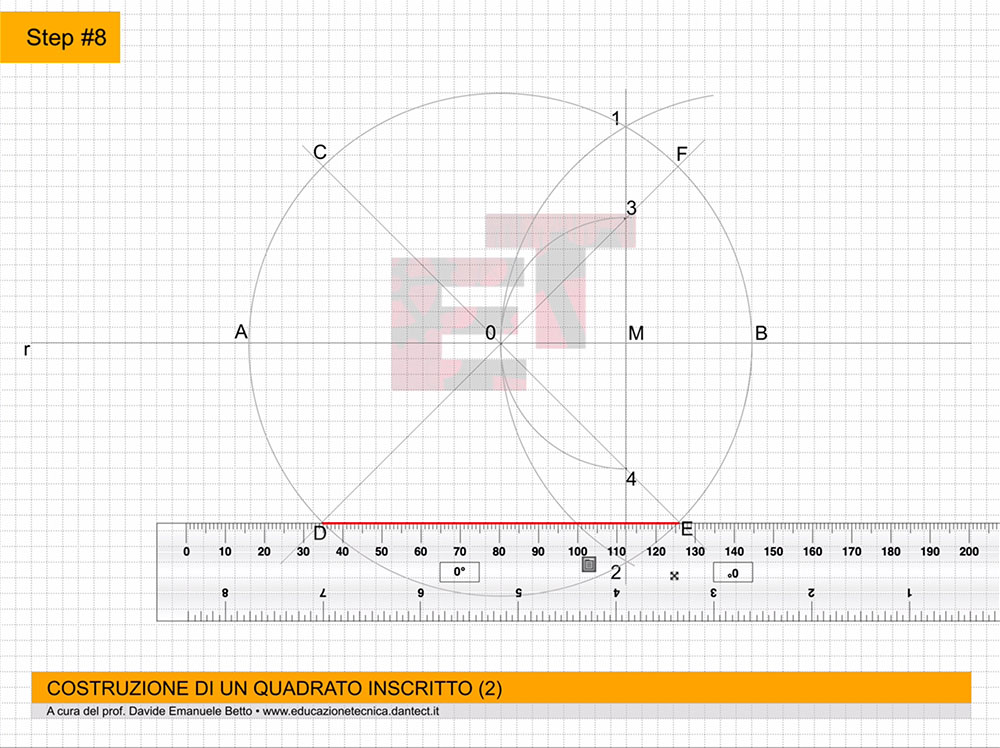
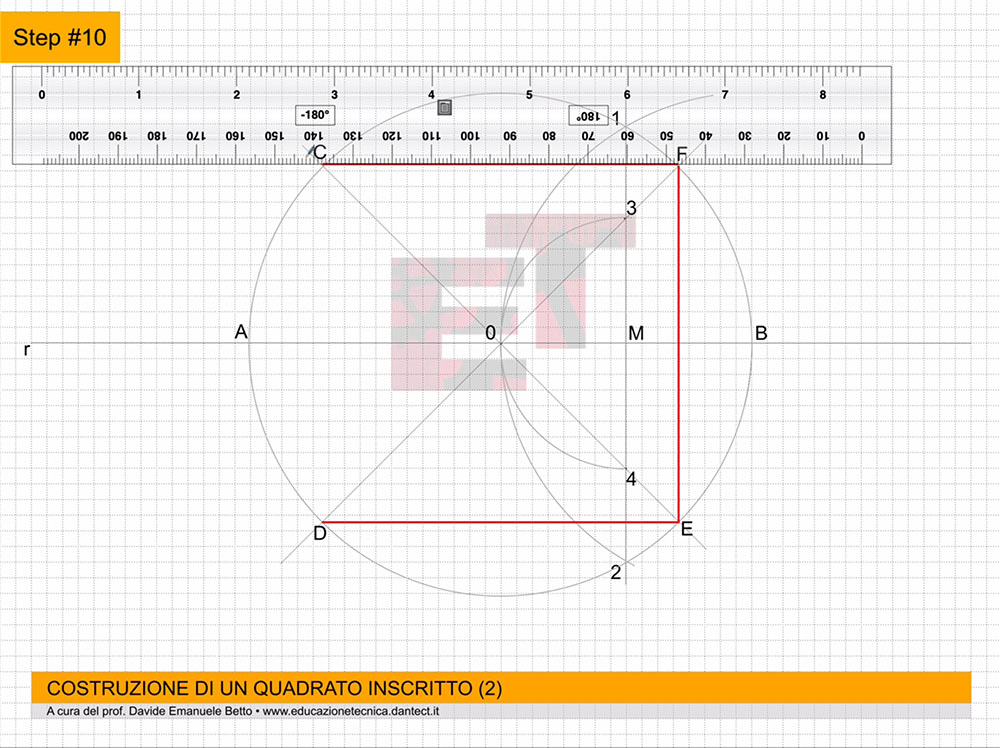
usando un foglio F4, posizionato in orizzontale, effettuiamo la sua squadratura secondo lo schema appreso (vedi SQUADRATURA).
In questa esercitazione, effettueremo le 3 Proiezioni Ortogonali di un quadrato di lato dato. Nella prima, il quadrato sarà posto parallelamente al Piano Orizzontale, nella seconda al Piano Verticale e nella terza al Piano Laterale. In ognuna di esse sarà fondamentale disegnare il quadrato al centro del piano a cui è parallelo.
| P.O. QUADRATO // AL PIANO ORIZZONTALE |
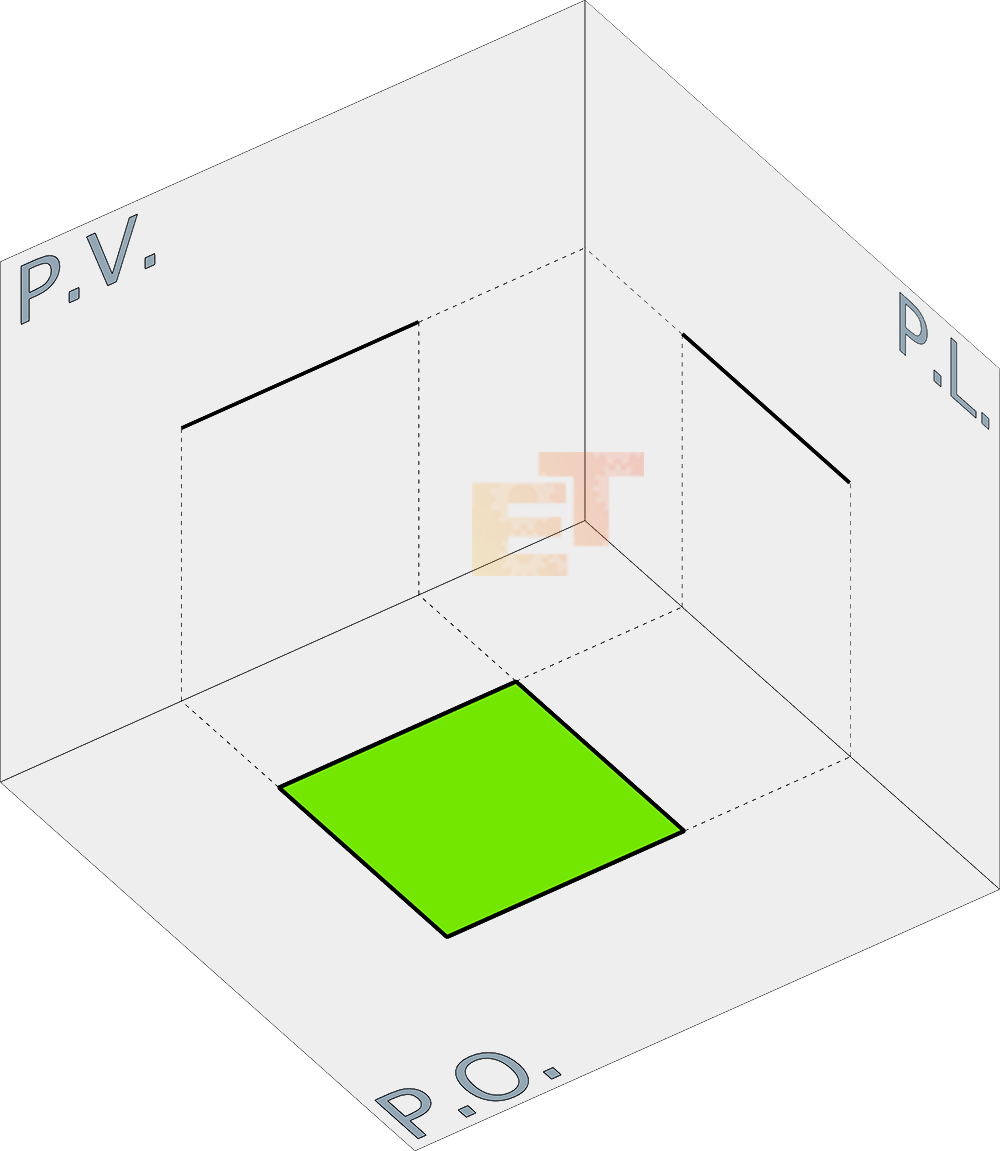
01 – Il quadrato posto parallelamente al Piano Orizzontale, ossia al piano che passa sotto i nostri piedi come il pavimento su cui camminiamo si trova nella posizione descritta sotto rispetto ai tre piani e proietta la sua superficie proprio sul Piano Orizzontale. Essendo una figura bidimensionale e non avendo per cui spessore, sugli altri due piani proietterà due linee di lunghezza pari al lato del quadrato.
01 – Quadrato parallelo al Piano Orizzontale
02 – Nell’immagine seguente, potete osservare le tre proiezioni del quadrato sui tre piani ortogonali.
02 – Proiezioni del quadrato di lato dato sui tre piani ortogonali
03 – Una volta che i 3 piani vengono ribaltati sul foglio da disegno trovandosi in posizione complanare, saremo in grado di disegnare le Proiezioni Ortogonali del quadrato sul foglio. Si dovrà partire dal quadrato sul Piano Orizzontale per poter poi determinare le proiezioni sui piani Verticale e Laterale che, come detto, saranno due segmenti di lunghezza pari al lato del quadrato.
03 – Proiezioni ortogonali di un Quadrato parallelo al Piano Orizzontale
- dividiamo l’area da disegno in quattro parti uguali tracciando un asse orizzontale e uno verticale;
- trascriviamo con il normografo i nomi dei diversi piani: P.O. (Piano Orizzontale), P.V. (Piano Verticale), P.L. (piano laterale);
- trascriviamo, inoltre, sull’asse orizzontale, all’inizio e alla fine le lettere L. e T. (Linea di Terra);
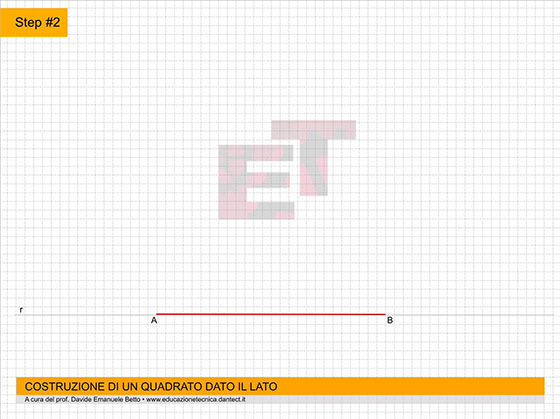
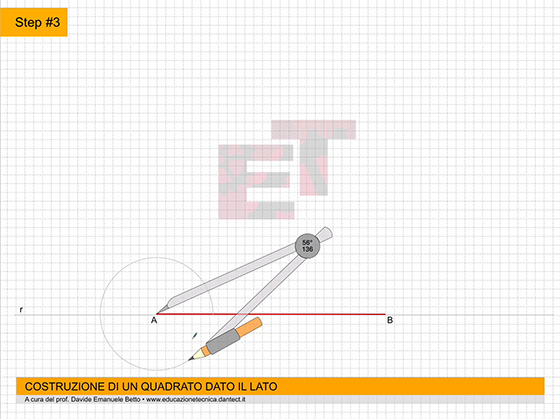
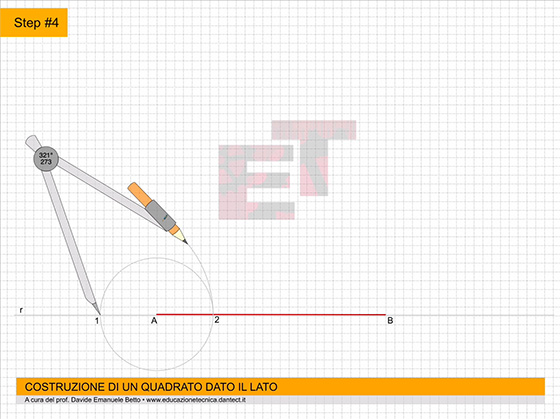
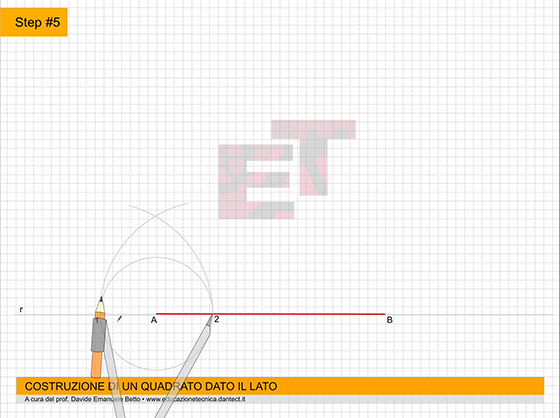
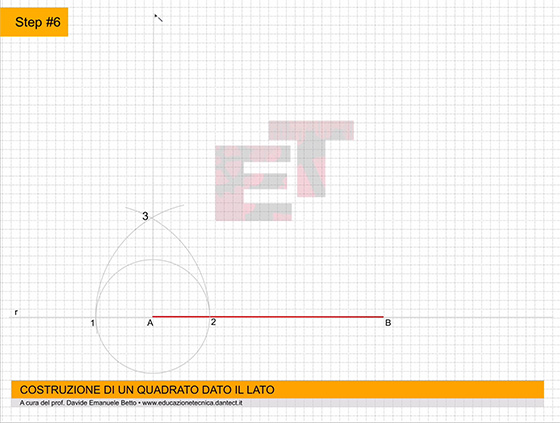
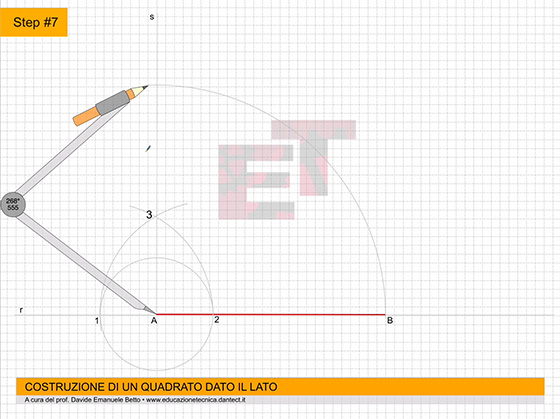
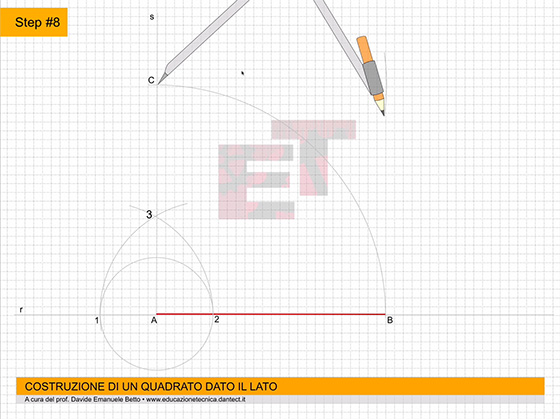
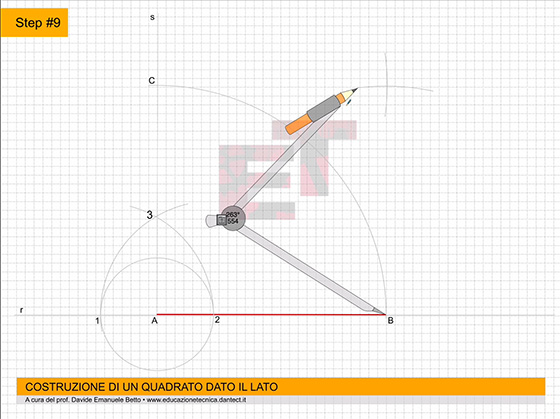
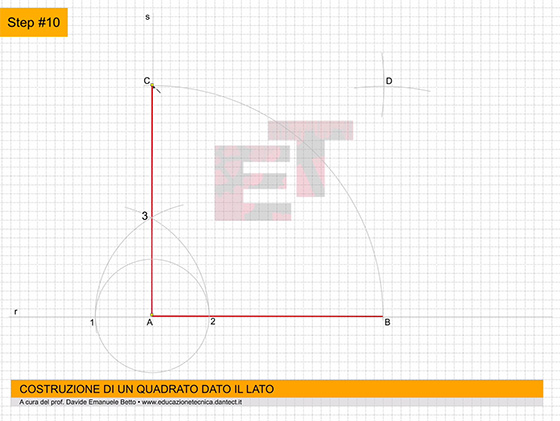
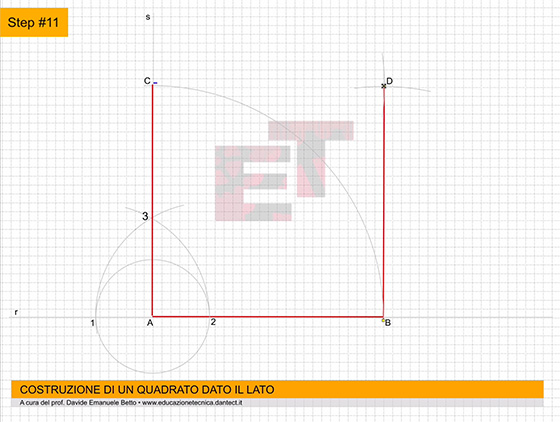
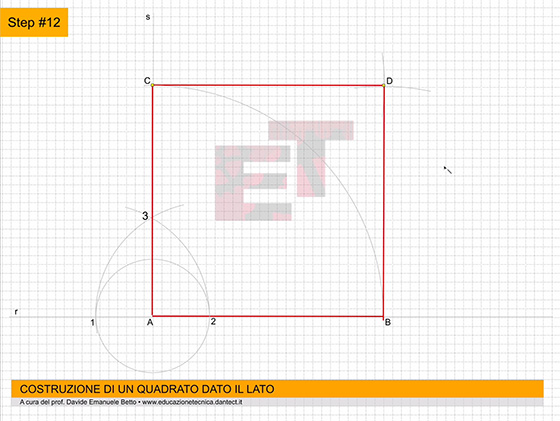
- costruiamo ora su P.O. il QUADRATO dato il lato utilizzando il metodo appreso precedentemente;
- nominiamo ogni vertice del quadrato ABCD;
- proiettiamo ciascuno spigolo ABCD ortogonalmente su P.V.;
- all’altezza indicata sui dati dell’esercitazione, tracciamo il segmento proiezione del quadrato ABCD sul Piano Verticale e inseriamo i nomi degli spigoli come in figura;
- proiettiamo ora ABCD su P.L.; per fare ciò dovremo proiettare gli spigoli del quadrato sull’asse verticale della costruzione. Poi puntando il compasso al centro degli assi ribaltiamo le proiezioni ABCD su L.T.;
- alziamo adesso le proiezioni all’altezza stabilita precedentemente (l’altezza su P.V. e su P.L. è la stessa) e colleghiamo le proiezioni su P.V. e su P.L.;
- per completare l’elaborato, rinforziamo solo le proiezioni del quadrato sui tre diversi piani (linee in rosso).
| P.O. QUADRATO // AL PIANO VERTICALE |
01 – Il quadrato posto parallelamente al Piano Verticale, ossia al piano posto di fronte a noi come una parete si trova nella posizione descritta sotto rispetto ai tre piani e proietta la sua superficie proprio sul Piano Verticale. Essendo una figura bidimensionale e non avendo per cui spessore, sugli altri due piani proietterà due linee di lunghezza pari al lato del quadrato.
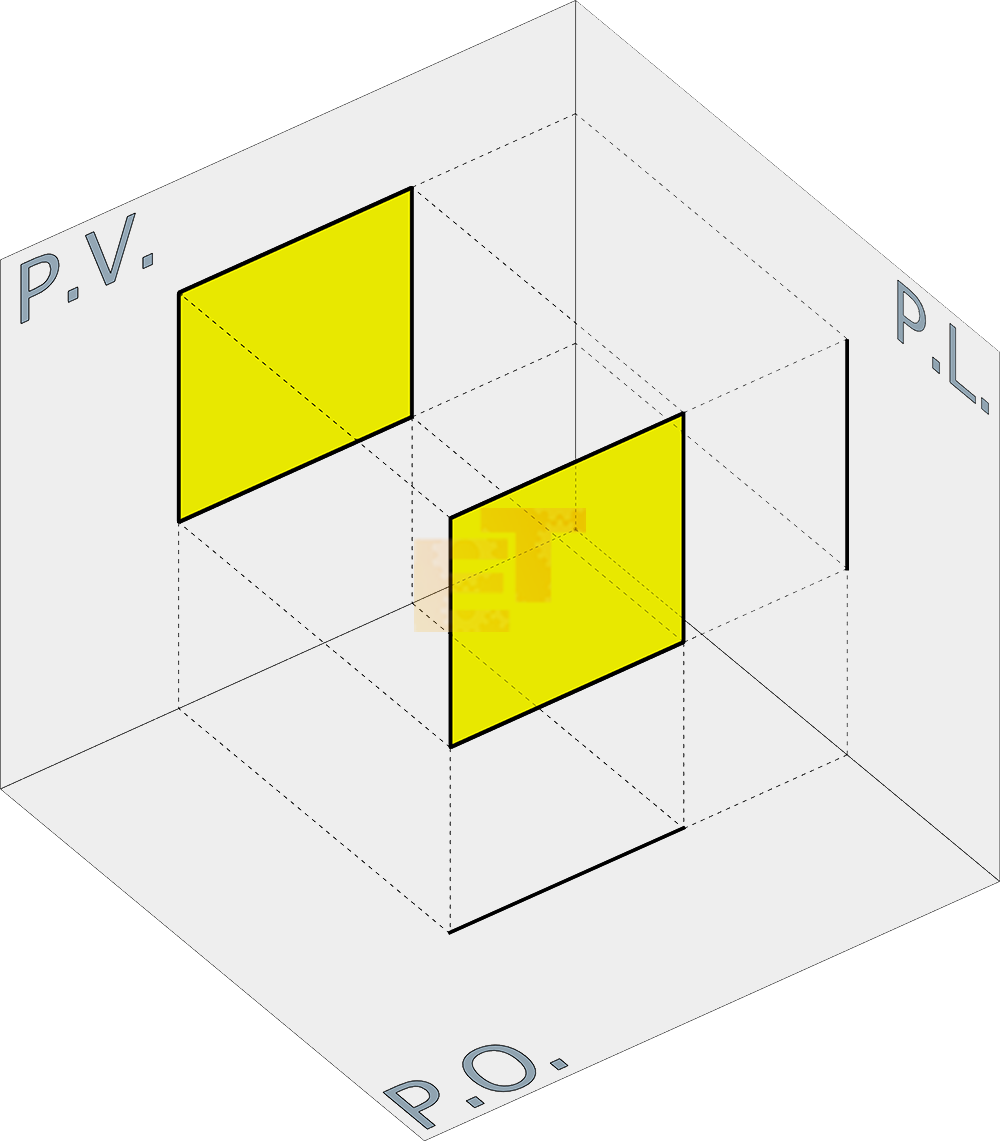
01 – Quadrato parallelo al Piano Verticale
02 – Nell’immagine seguente, potete osservare le tre proiezioni del quadrato sui tre piani ortogonali.
02 – Proiezioni del quadrato di lato dato sui tre piani ortogonali
03 – Una volta che i 3 piani vengono ribaltati sul foglio da disegno trovandosi in posizione complanare, saremo in grado di disegnare le Proiezioni Ortogonali del quadrato sul foglio. Si dovrà partire dal quadrato sul Piano Verticale per poter poi determinare le proiezioni sui piani orizzontale e laterale che, come detto, saranno due segmenti di lunghezza pari al lato del quadrato.
03 – Proiezioni ortogonali di un Quadrato parallelo al Piano Verticale
| P.O. QUADRATO // AL PIANO LATERALE |
01 – Il quadrato posto parallelamente al Piano Laterale, ossia al piano posto alla nostra destra come la parete di una stanza posta lateralmente a noi, si trova nella posizione descritta sotto rispetto ai tre piani e proietta la sua superficie proprio sul Piano Laterale. Essendo una figura bidimensionale e non avendo per cui spessore, sugli altri due piani proietterà due segmenti di lunghezza pari al lato del quadrato.
01 – Quadrato parallelo al Piano Laterale
02 – Nell’immagine seguente, potete osservare le tre proiezioni del quadrato sui tre piani ortogonali.
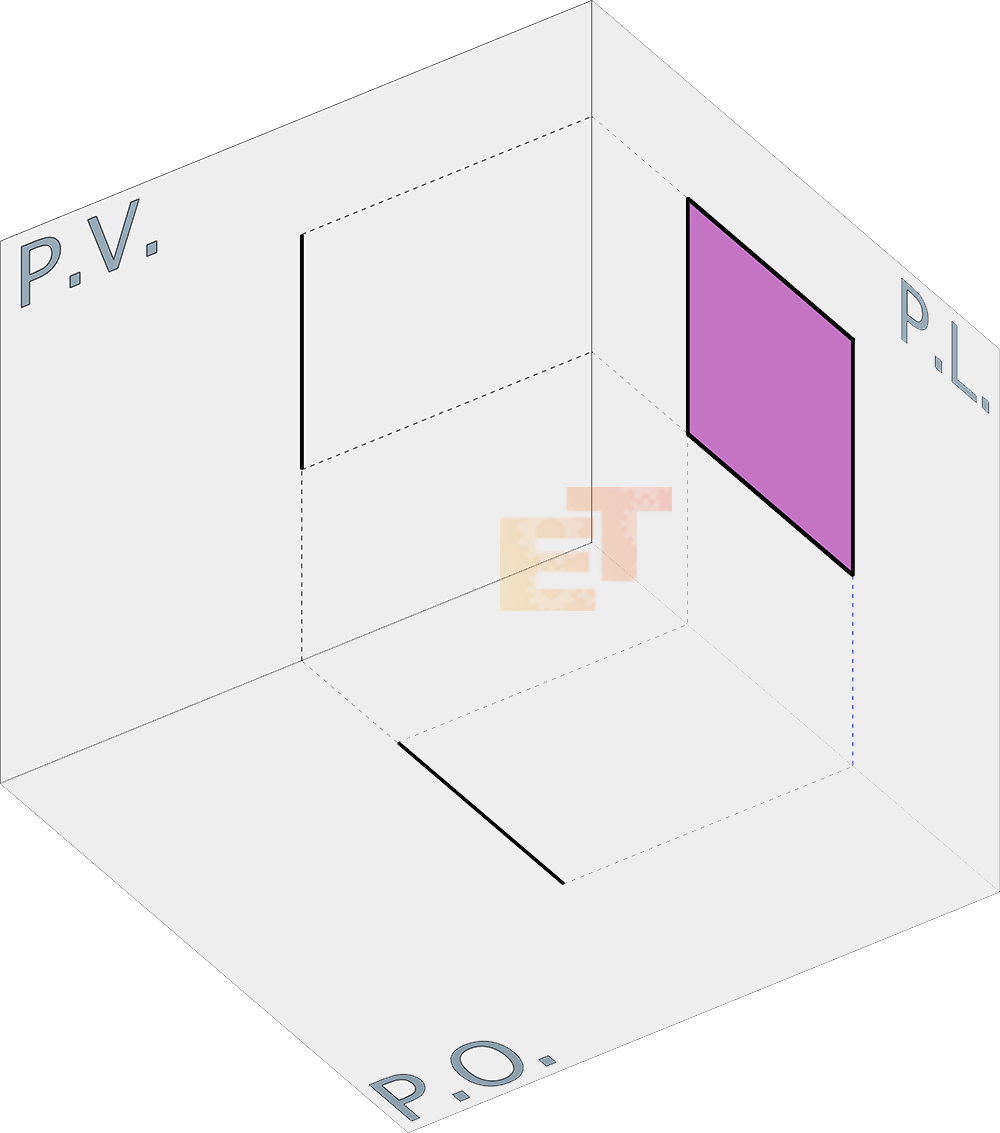
02 – Proiezioni del quadrato di lato dato sui tre piani ortogonali
03 – Una volta che i 3 piani vengono ribaltati sul foglio da disegno trovandosi in posizione complanare, saremo in grado di disegnare le Proiezioni Ortogonali del quadrato sul foglio. Si dovrà partire dal quadrato sul Piano Laterale per poter poi determinare le proiezioni sui piani Orizzontale e Verticale che, come detto, saranno due segmenti di lunghezza pari al lato del quadrato.
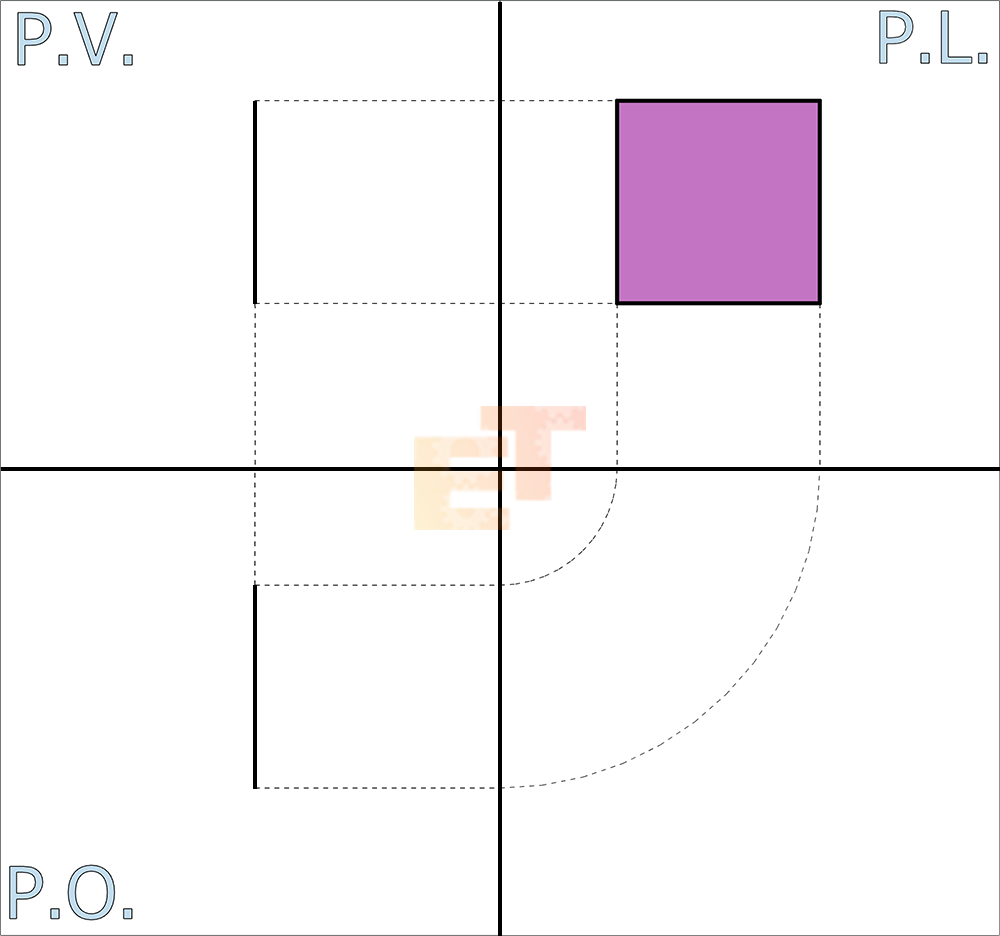
03 – Proiezioni ortogonali di un Quadrato parallelo al Piano Laterale
Questo esercizio non dispone di tutorial esplicativi perché presuppone la conoscenza delle tecniche di consegna. Si consiglia, quindi, di assegnarlo solo dopo aver fatto svolgere diversi esercizi e solo quando si riterranno i propri alunni capaci di poterlo svolgere autonomamente.
Tutorial video: 
