 |
SEZIONE AUREA SEGMENTO |
| Dati | LUNGHEZZA SEGMENTO 10cm o secondo indicazione del docente |
| CONSEGNE: | |
| Consegna 1 | Esegui la costruzione geometrica come spiegato nel tutorial |
| Digit | Esegui le consegne in digitale utilizzando il CAD |
| DIFFICOLTA’ e CLASSE: | |
| Livello | Classe |
|
| STRUMENTI NECESSARI: |
 |
| DESCRIZIONE: |
Prima di iniziare, pulisci il piano di lavoro e gli strumenti da disegno. Usando un foglio F4 liscio, effettua la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le consegne.
| DEFINIZIONE DI SEZIONE AUREA O NUMERO DIVINO |
Prima di procedere alla costruzione, bisogna fare chiarezza su cosa sia la sezione aurea. Fin dai tempi più antichi, dagli egiziani, ci si è resi conto che esiste una proporzione divina o sezione aurea tra le misure, capaci di far ottenere oggetti le cui misure siano armoniche tra di loro. Questa proporzione, studiata fin dall’antichità è applicata all’architettura, alla pittura, alla musica, corrisponde ad un rapporto pari a 1,618 chiamato anche il numero d’oro. In tanti hanno utilizzato questa proporzione per creare oggetti e immagini armoniche. La piramide egizia di Cheope, i megaliti di Stonehenge, il Partenone di Atene, la cattedrale di Notre Dame nonché opere pittoriche come la Gioconda di Leonardo o la Venere del Botticelli, sono costruite su questa proporzione utilizzando il numero d’oro.
L’utilizzo di questa proporzione continua anche ai giorni nostri basti pensare che oggetti d’uso comune come le carte di credito, o le sim dei cellulari, sono tutti dei rettangoli aurei con rapporto tra base altezza pari a 1,618.

In pratica dato un segmento A-C, si ottiene la sua sezione aurea quando il suo tratto più corto B-C sta al tratto più lungo A-B, come questo sta al segmento intero A-C. Questo rapporto viene espresso attraverso la seguente proporzione:
BC : AB = AB : AC = 1,618
Costruiamo adesso geometricamente la sezione aurea di una segmento.
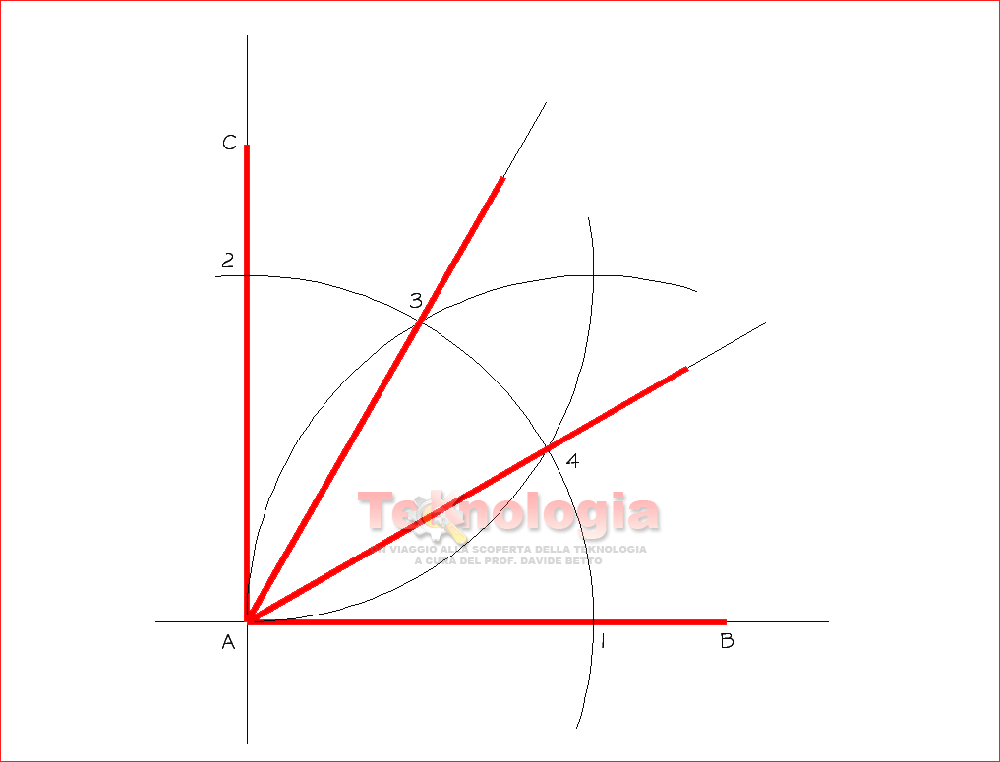
| FIGURA DI RIFERIMENTO: |
| PROCEDURA OPERATIVA |
posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:
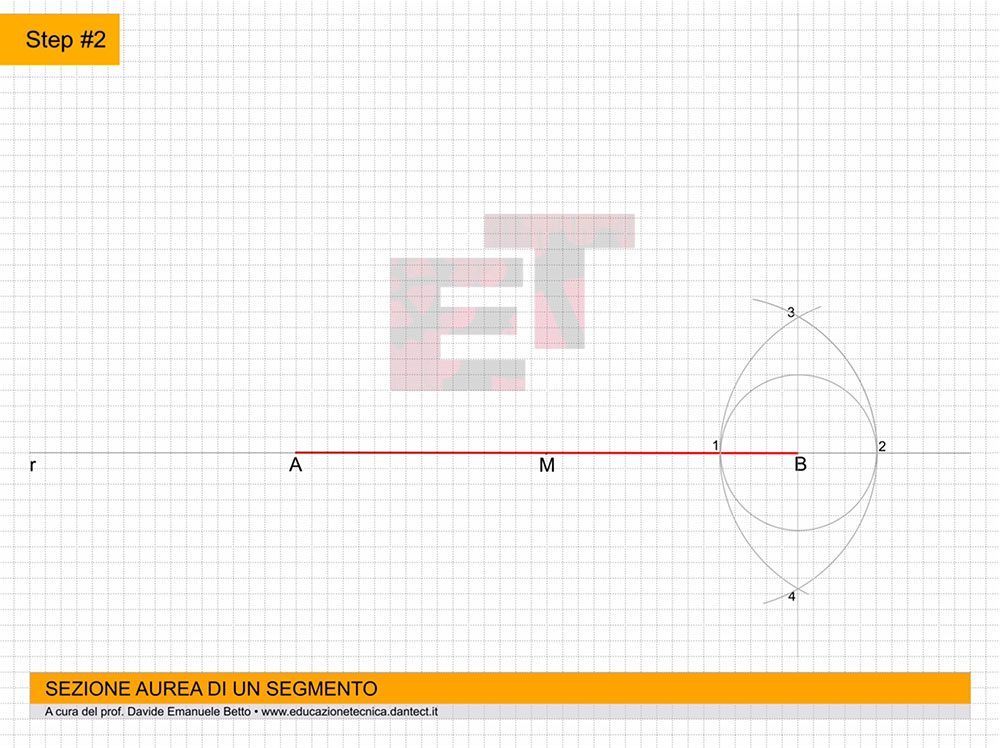
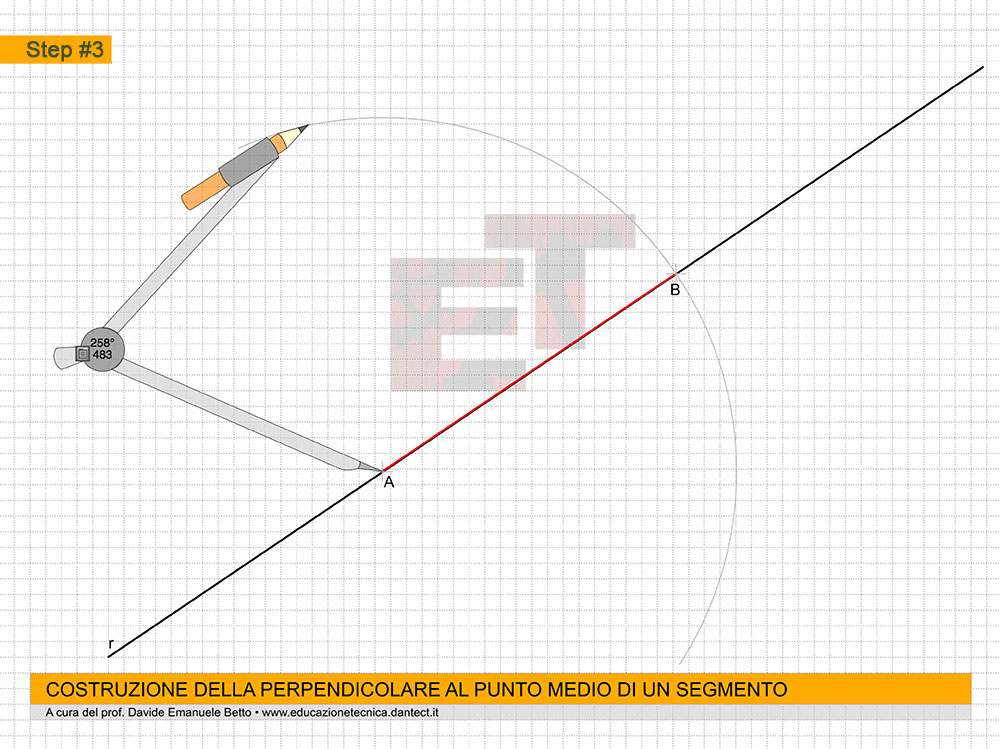
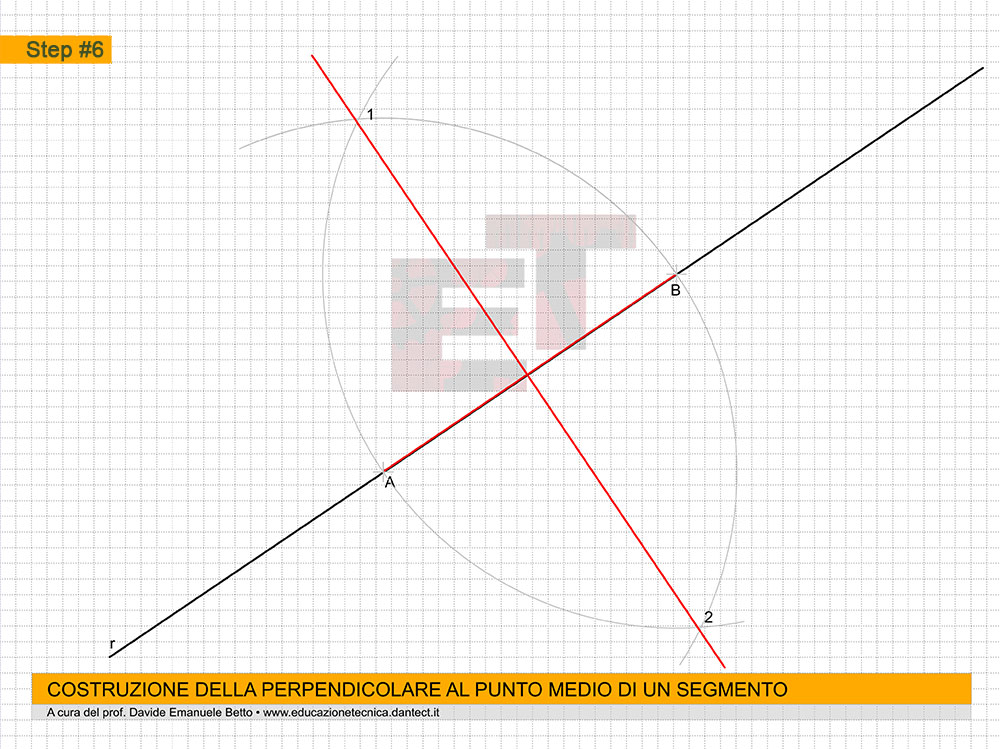
Step #1 – tracciamo una retta r e individuiamo su di essa un segmento A-B di dimensione data. Indichiamo inoltre sul segmento A-B il suo punto medio M (vedi: PERPENDICOLARE AL PUNTO MEDIO DI UN SEGMENTO);
Step #2 – tracciamo adesso da B la perpendicolare al segmento A-B utilizzando il metodo già appreso (vedi: PERPENDICOLARE ALL’ESTREMO DI UN SEGMENTO);
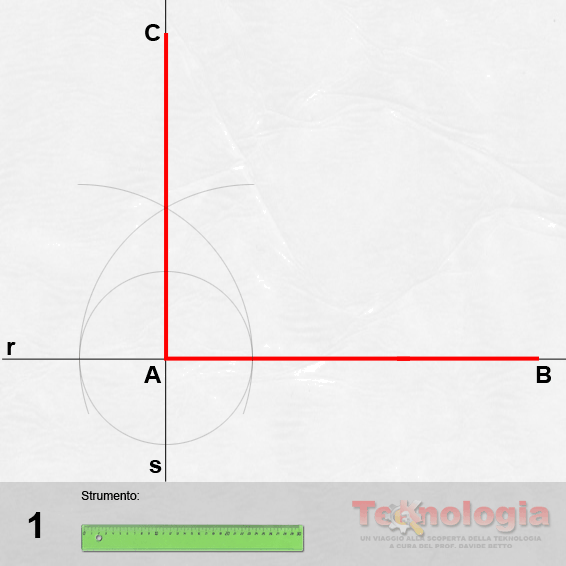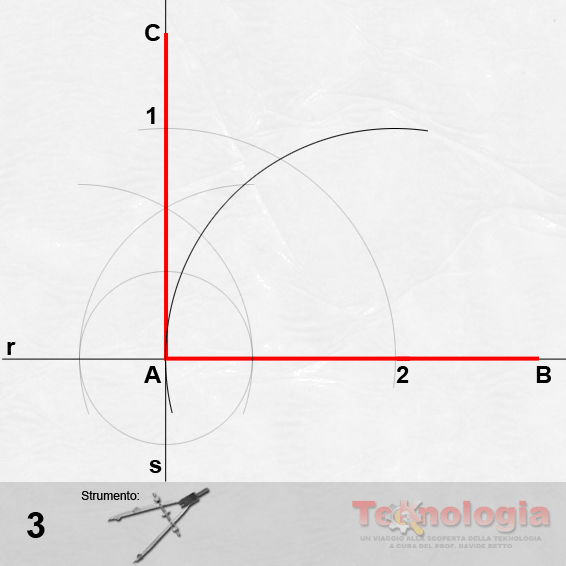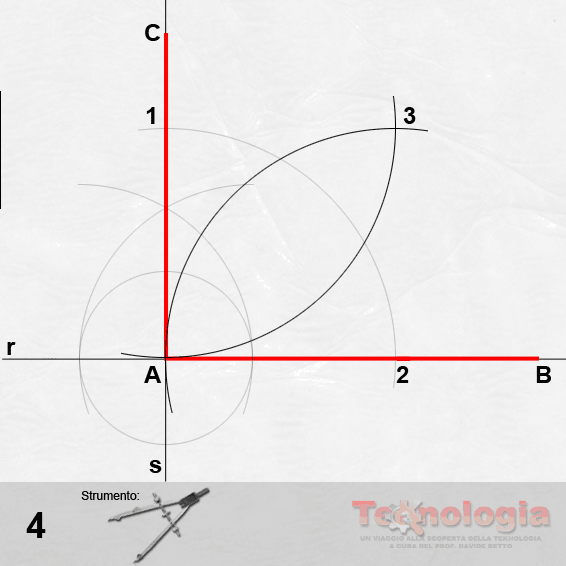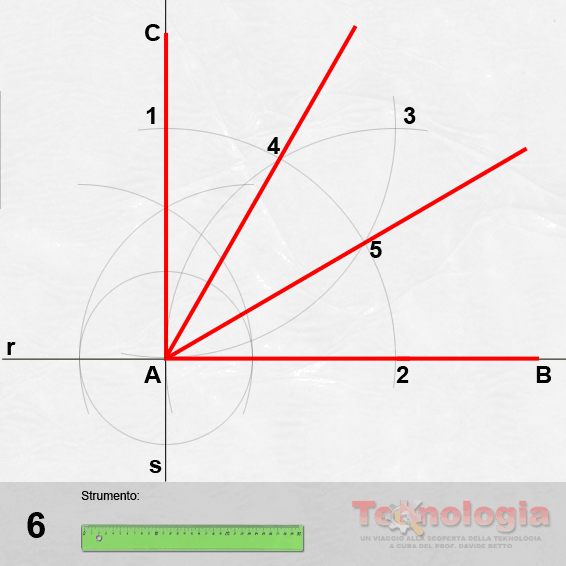
Step #3 – puntiamo il compasso in B e con apertura B-M tracciamo un arco che intersecherà la perpendicolare ad A-B in un punto che chiameremo C;
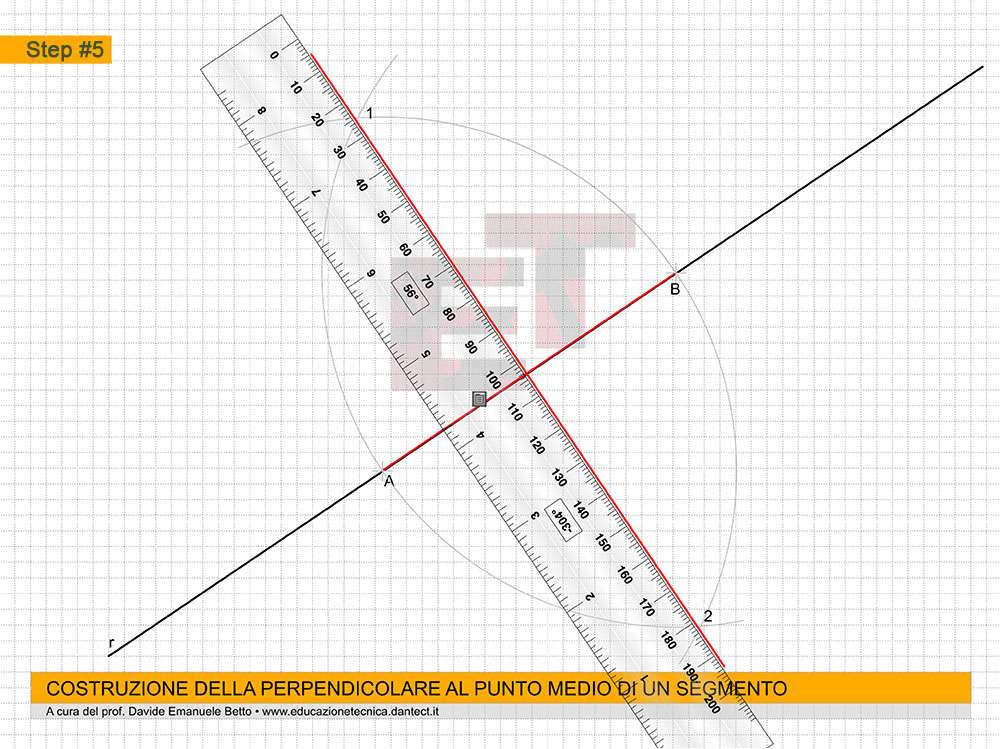
Step #4 – con un righello, uniamo il punto A con il punto C;
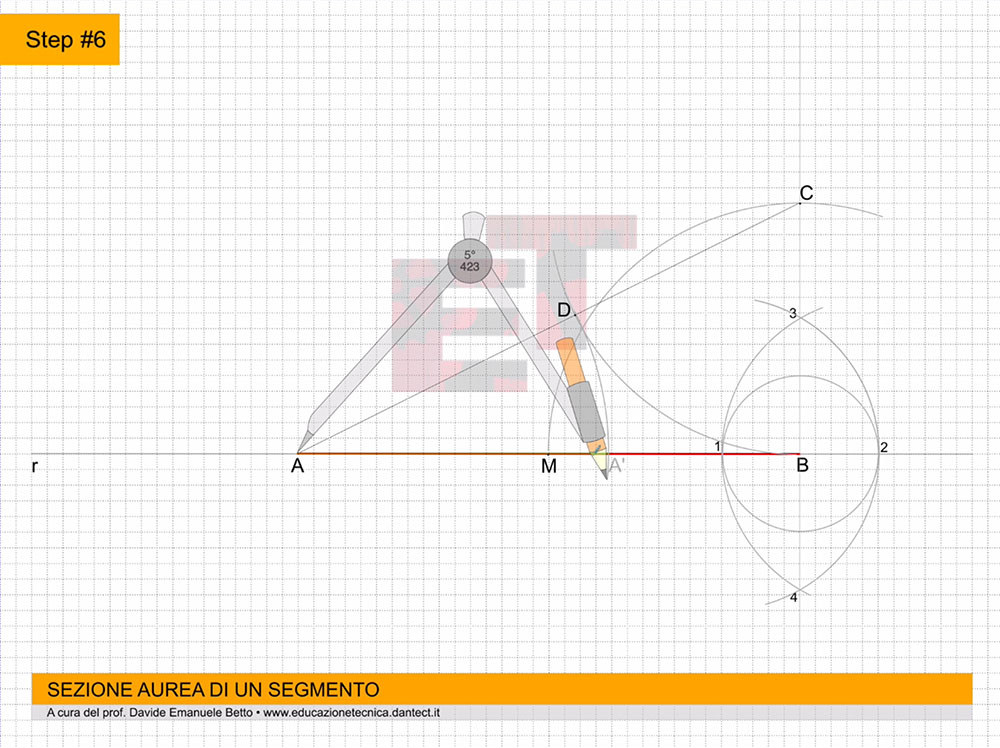
Step #5 – puntiamo adesso il compasso in C e con apertura C-B tracciamo un arco che intersecherà la congiungente A-C in un punto che chiameremo D;
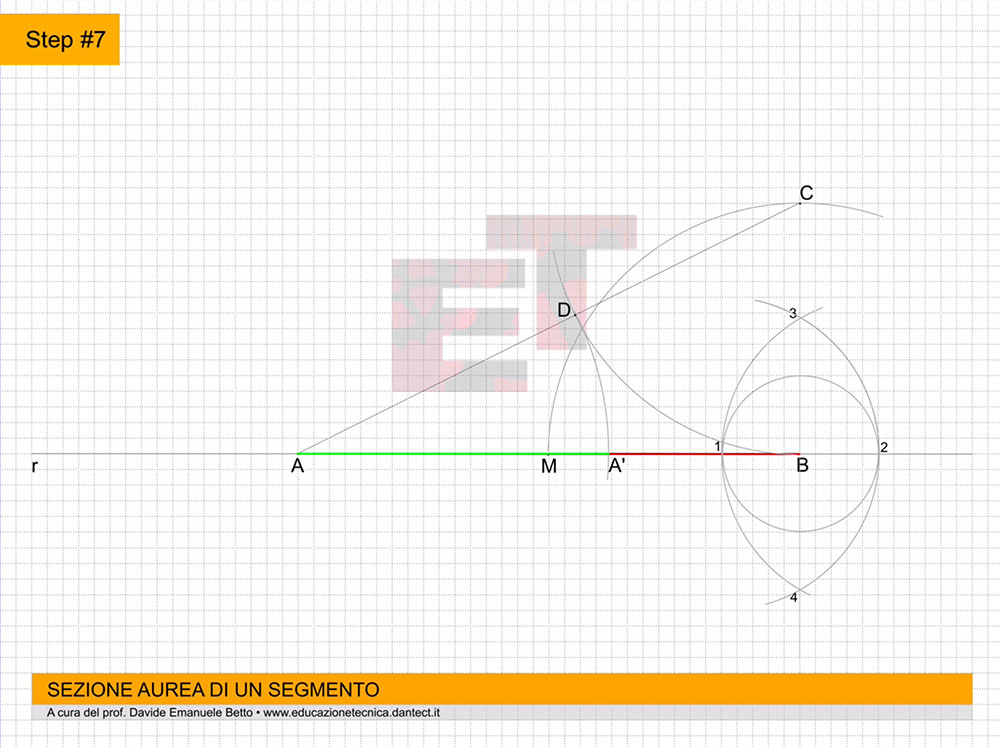
Step #6 –infine, puntiamo il compasso in A e con apertura A-D, tracciamo un arco che intersecherà il segmento A-B in un punto A’;
Step #7 – la distanza A-A’ rappresenta la sezione aurea del segmento A-B.
Ricordo che le linee colorate di rosso e verde sono quelle che vanno rinforzate nel disegno.
| TUTORIAL VIDEO |