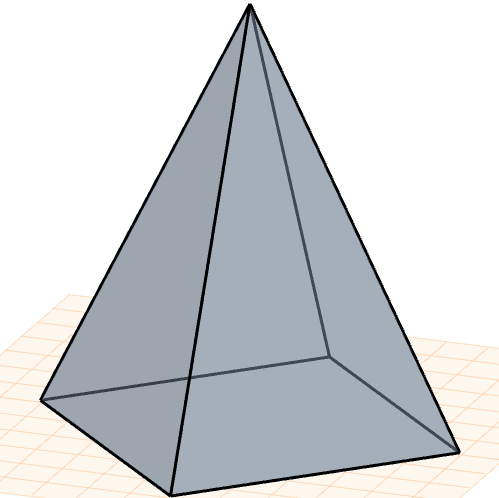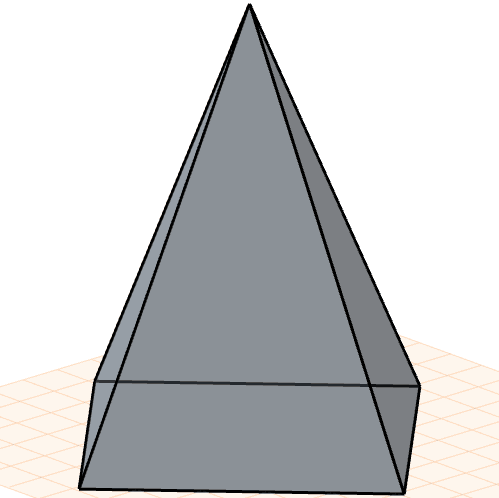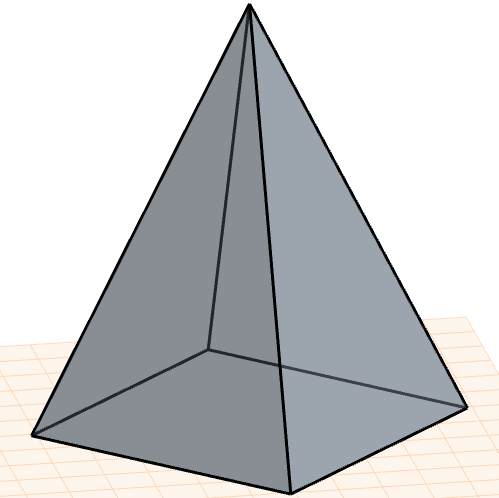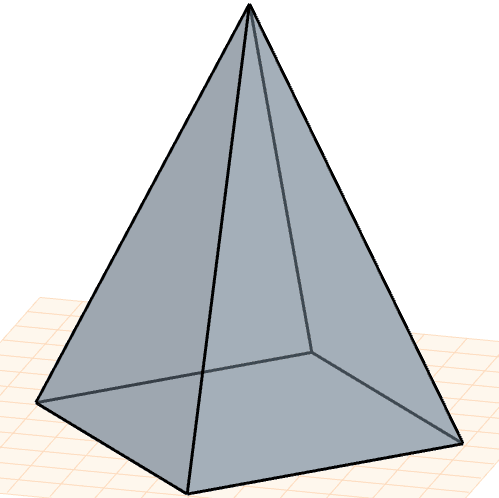
La PIRAMIDE è una figura geometrica solida avente una base e un vertice.
La base è poligonale, quindi cambia forma a seconda della figura geometrica che la definisce (avremo quindi piramidi triangolari, quadrate, pentagonali, ecc.), mentre il vertice non giace sullo stesso piano della base. Unendo gli spigoli della figura di base con il vertice, si generano altre figure geometriche chiamate facce laterali che nella piramide sono tutte triangoli; quindi, una piramide avrà tante facce laterali quanti sono i lati della figura di base per cui una piramide a base triangolare avrà 4 facce, una di base e 3 in elevazione, mentre una piramide a base quadrata ne avrà 5, una di base e 4 in elevazione e così via.
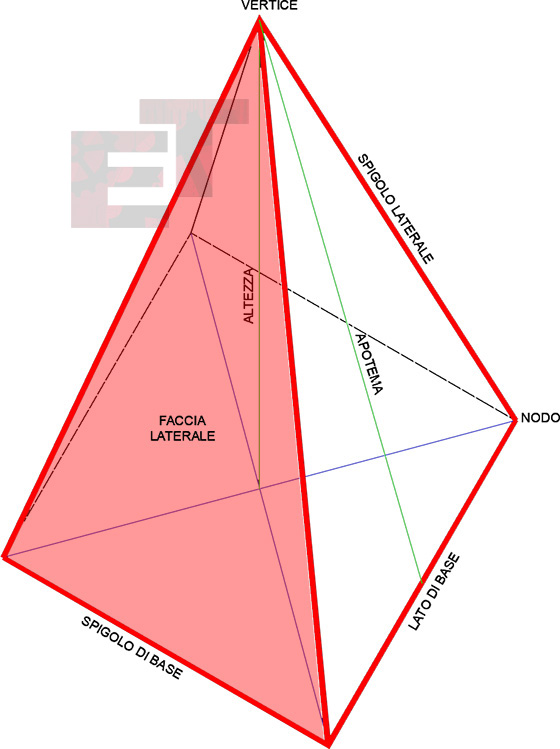
In geometria, è definita un poliedro limitato da un poligono, detto base, e da tanti triangoli quanti sono i lati del poligono, tutti aventi un vertice in comune, detto vertice o apice della piramide. Si definiscono facce della piramide, la sua base e le facce laterali triangolari che convergono sull’apice.
Si definisce altezza della piramide, la distanza fra il suo vertice e il piano che contiene la base.
Gli spigoli che limitano il poligono di base si chiamano spigoli di base, mentre quelli che delimitano le facce laterali, si chiamano spigoli laterali.
Si definisce superficie laterale di una piramide, l’insieme delle sue facce laterali, e superficie totale l’insieme di queste e la superficie della base.
L’altezza comune a tutte le facce laterali di una piramide retta si chiama apotema della piramide.
Una piramide si dice retta quando nella sua base si può inscrivere una circonferenza il cui centro è il piede dell’altezza della piramide. Una piramide si definisce regolare se è retta e quando la sua base è formata da un poligono regolare.
Si chiama tronco di piramide, una piramide tagliata da un piano parallelo alla base. La base della piramide e il poligono generato dalla sezione prendono il nome di basi del tronco di piramide; avremo così una base maggiore che coincide con la figura di base della piramide e una base minore che coincide con il piano di taglio. La distanza tra le due basi è detta altezza del tronco di piramide.
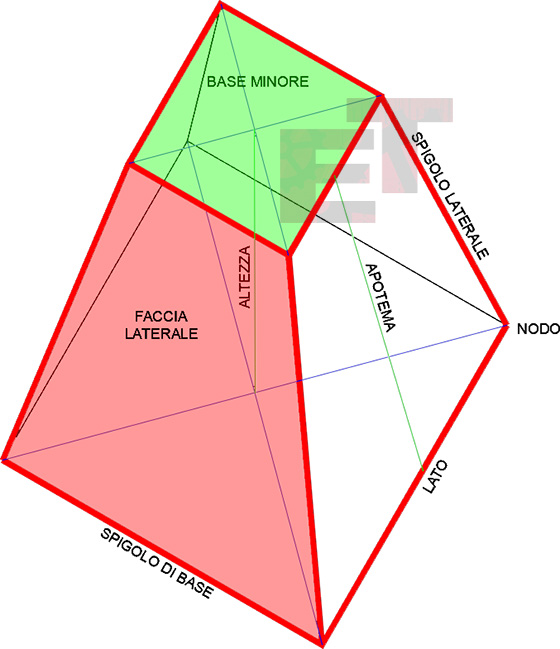
Un tronco di piramide si dice retto o regolare se è stato ottenuto da una piramide retta o regolare.
In un tronco di piramide regolare le facce laterali sono trapezi isosceli congruenti la cui altezza è detta apotema del tronco.
Di seguito alcuni esempi di piramidi regolari. Clicca sui links per approfondimenti.
Il termine piramide deriva dalla parola greca pyramis cioè di una pietanza a base di grano che aveva la forma simile ad una piramide.
Gli esempi più importanti di piramidi nella storia sono sicuramente le costruzioni egizie a Giza nelle loro diverse espressioni e soluzioni, la cui funzione era quella di monumento funerario. Seguono, poi, le piramidi Maya che venivano invece utilizzate come templi religiosi. Soluzione moderna altrettanto famosa la ritroviamo a Parigi nel Louvre, dove una gigantesca piramide di vetro realizza l’ingresso al nuovo museo.
-
-
Saqqara (Egitto)
-
-
Dahshur (Egitto)
-
-
Giza (Egitto)
-
-
Chicken Itza (Messico)
-
-
Tikal Gran Jaguar (Guatemala)
-
-
Cestia (Roma)
-
-
Louvre (Parigi)
Questo articolo è stato realizzato in collaborazione con la prof.ssa Carmela Milone docente di Matematica, nonché amica e autorevole voce scientifica scolastica.
Questo esercizio non dispone di tutorial esplicativi perché presuppone la conoscenza delle tecniche di consegna. Si consiglia, quindi, di assegnarlo solo dopo aver fatto svolgere diversi esercizi e solo quando si riterranno i propri alunni capaci di poterlo svolgere autonomamente.
Tutorial video: 
